Batch Coolingの式（冷却水出口温度が一定ではない場合）

ここでは，冷却時間の計算式を紹介します。

「スケールアップ理論を考えてみよう ー 冷却編【冷却モデル】」のページで，冷却水による製品の冷却モデルを考えました。

ジャケット冷却する際に，Batch Coolingの式によって冷却時間を算出できることが知られています。

Batch Coolingの式はいろいろな表し方がありますが，ここでは冷却水出口温度が一定ではない場合を採用します。

”冷却水出口温度が一定ではない場合”とは，冷却水出口温度が60℃，50℃…というように変化することを意味します。

📝[memo]　今回の事例では，常に冷却水出口温度が一定になるということはありませんよね。

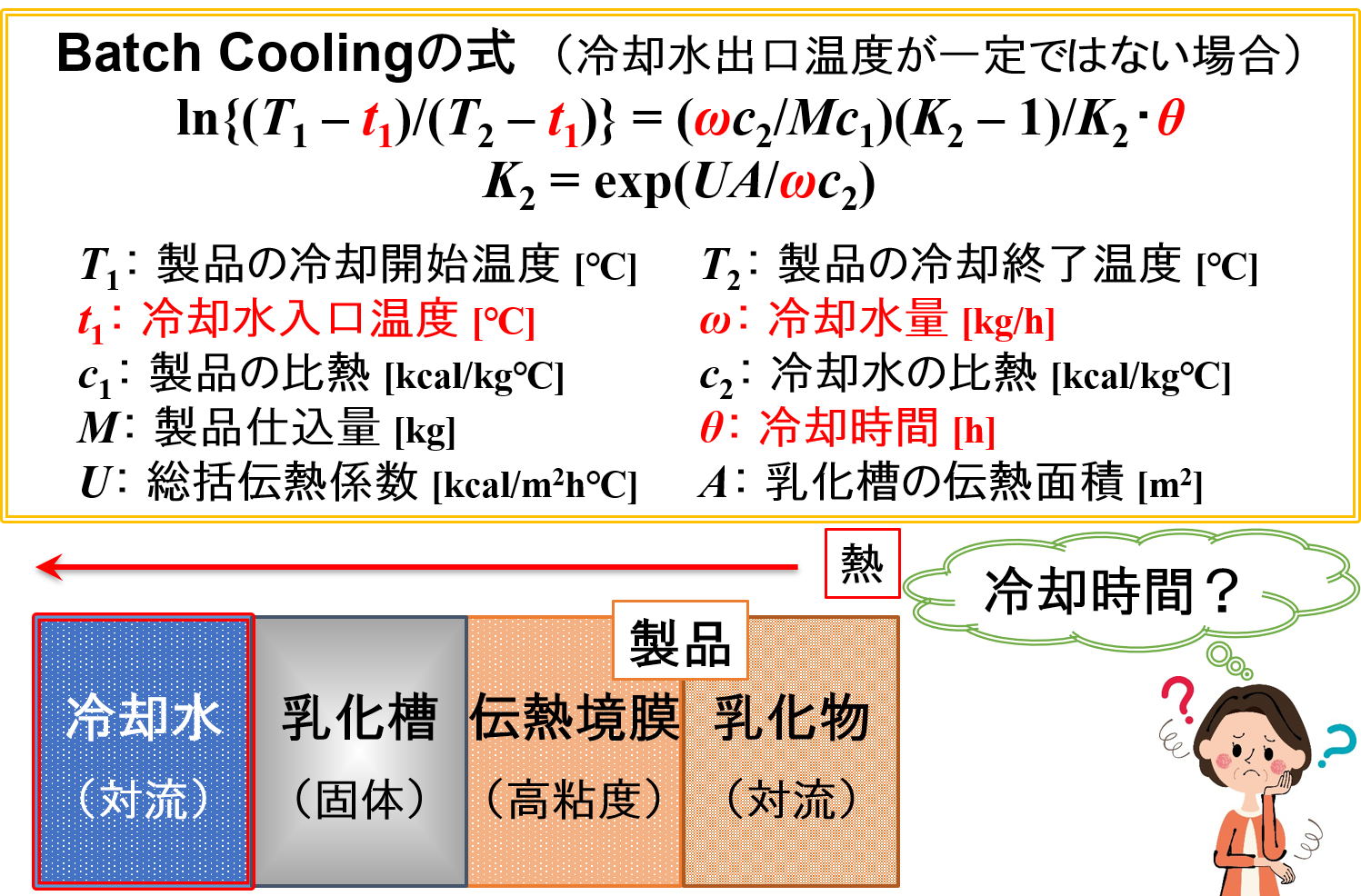
冷却時間を決める因子

Batch Coolingの式の形を見てみましょう。最終的に知りたいのは冷却時間θです。

このとき，使用する乳化槽は決まっています。

したがって，製品仕込量M，総括伝熱係数U，乳化槽の伝熱面積Aは定数となります。（変化しません）

📝[memo]　総括伝熱係数Uは変化する可能性がありますが，ここでは変化しないとみなして話を進めることにします。

また，製造する製品も決まっています。

したがって，製品の冷却開始温度T₁，製品の冷却終了温度T₂，製品の比熱c₁は定数となります。（変化しません）

次に，冷却水の条件を考えてみましょう。

冷却水のユーティリティが決まっているとすると，冷却水の比熱c₂は定数となります。（変化しません）

一方で，冷却水の使い方によって，冷却水入口温度t₁，冷却水量ωを変えることができます。

すなわち，冷却時間θは冷却水入口温度t₁と冷却水量ωによって決まると言えそうです。

ここでは，比熱cや総括伝熱係数Uに関して，単位として”kcal”を使用しています。

慣習的に昔の単位系をそのまま使うことが多いので，ここでは非SI単位系とさせてください。

Batch Coolingの式の導出

一応，Batch Coolingの式を導出するまでの流れを紹介したいと思います。

難しいと思われた方は，飛ばしても全然問題ありません。

むしろ，この式を使って実務に活かすことを重視しましょう。

① 製品から奪われる熱　dq/dθ = –Mc₁dT/dθ

② 冷却水が得る熱　dq/dθ = ωc₂(t₂ – t₁)

③ ジャケット冷却により移動する熱　dq/dθ = UAΔt

Δt は後述する数平均温度差です。

②③は等しいので，ωc₂(t₂ – t₁) = UAΔt …(1)

①②は等しいので，–Mc₁dT/dθ = ωc₂(t₂ – t₁) …(2)

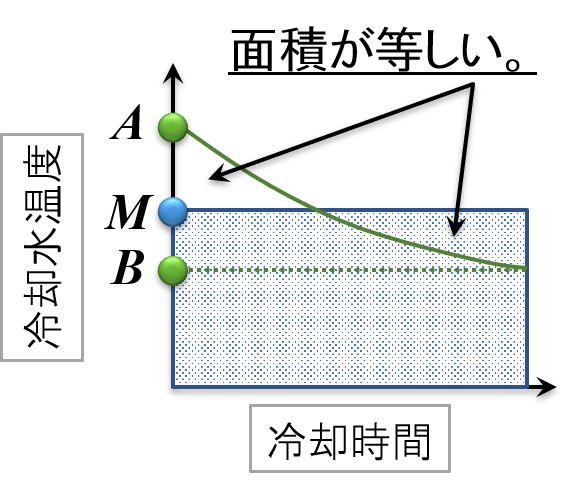
製品温度Tにおける対数平均温度差

Δt = (t₂ – t₁)/ln{(T – t₁)/(T – t₂)} …(3)

ここで，対数平均温度差についてイメージを紹介します。

📝[memo]　詳細な説明は専門書にお任せしますので，あくまでもイメージ留めています。

今回のケースを想定した冷却をするとき，右図で示すように，冷却水出口の温度（開始Aと終了B）は指数関数となることが知られています。

そのため，グラフの両端（開始Aと終了B）のみで平均値Mを求めることができます。

すると，冷却中の冷却水出口は常に温度Mになっているとみなすことができます。

式(3)を式(1)に代入

ωc₂(t₂ – t₁) = UAΔt = UA(t₂ – t₁)/ln{(T – t₁)/(T – t₂)}

⇔ ln{(T – t₁)/(T – t₂)} = UA/ωc₂

⇔ (T – t₁)/(T – t₂) = exp(UA/ωc₂) = K₂

⇔ t₂ = T + (t₁ – T)/K₂ …(4)

製品温度Tにおける冷却水出口温度t₂を算出できます。

式(4)を式(2)に代入

–MC₁dT/dθ = ωc₂(t₂ – t₁) = ωc₂{T + (t₁ – T)/K₂ – t₁} = (K₂ – 1)/K₂・(T – t₁)

⇔ Mc₁dT/dθ = (K₂ – 1)/K₂・(t₁ – T)

⇔ dT/(t₁ – T) = (ωc₂/MC₁)(K₂ – 1)/K₂・dθ

⇔ ∫dT/(t₁ – T) = ∫(ωc₂/MC₁)(K₂ – 1)/K₂・dθ

⇔ ln{(T₁ – t₁)/(T₂ – t₁)} = (ωc₂/MC₁)(K₂ – 1)/K₂・θ

このようにして，Batch Coolingの式が得られます。

冷却水（温度・量の影響）

ここで，当社の乳化撹拌装置にこのBatch Coolingの式を適用したとき，どのようなことがわかるでしょうか？

当社の200型基準機を例に考えてみましょう。

ただし，冷却中の総括伝熱係数と製品温度は，常に一定であると仮定して計算してみます。

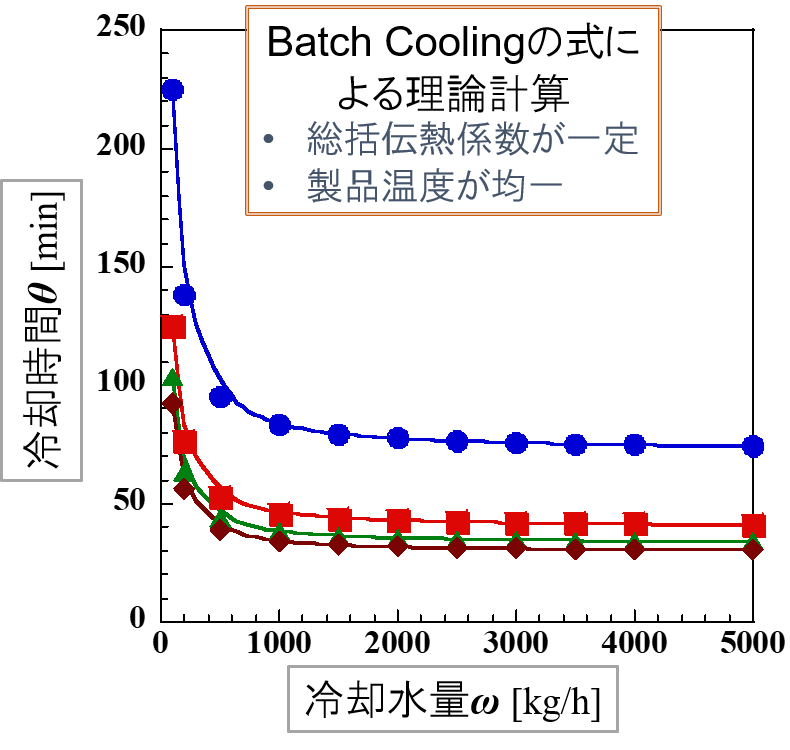
以下の冷却条件で計算すると，右図の結果が得られます。

冷却水入口温度の違いは，4点（● ■ ▲ ◆）で表しています。

そして，縦軸は「冷却時間」，横軸は「冷却水量」を示します。

• 製品仕込量： 150 [kg]
• 製品の比熱： 1 [kcal/kg℃]
• 製品温度： 80 [℃] → 30 [℃]
• 総括伝熱係数： 260 [kcal/m²h℃]

●： 冷却水入口温度t₁ = 25 [℃]

■： 冷却水入口温度t₁ = 12 [℃]

▲： 冷却水入口温度t₁ = 5 [℃]

◆： 冷却水入口温度t₁ = 0 [℃]

冷却水入口温度t₁に着目したとき

いずれの冷却水量においても，冷却水入口温度が低い方が冷却時間は短くなっています。

ただし，冷却水入口温度を低くすればするほど，冷却時間は劇的に短くなるというわけではありません。

ある温度以下で一定とみなせるようになります。

冷却水量ωに着目したとき

いずれの冷却水入口温度においても，冷却水量が大きい方が冷却時間は短くなっています。

ただし，冷却水量を大きくすればするほど，冷却時間は劇的に短くなるというわけではありません。

ある量以上で一定とみなせるようになります。

このように考えると，設備投資に要する費用（冷却水入口温度を低くする，冷却水量を大きくする）と実際の製品の冷却時間を鑑みて，実用的な冷却条件を決めていくことになります。

📝[memo]　①冷却水入口温度を低くする，②冷却水量を大きくすると冷却時間が短くなるのは容易に想像できますが，実際は限界があるということですね。

製品仕込量と冷却時間の目安（当社基準）

今度は，当社の乳化撹拌装置で製品を冷却するとき，製品仕込量と冷却時間の関係を調べます。

ただし，冷却中の総括伝熱係数と製品温度は，常に一定であると仮定して計算してみます。

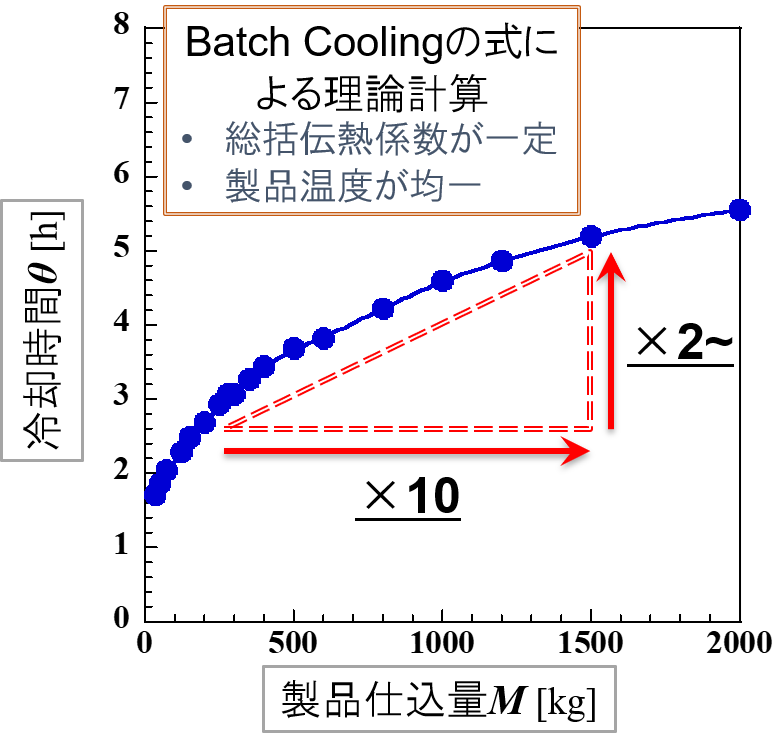
以下の冷却条件で計算すると，右図の結果が得られます。

ここに記載されていない種々の条件は，当社の標準仕様に従います。

📝[memo]　当社の技術情報になるので，オープンにできない内容は記載を省略しています。

そして，縦軸は「冷却時間」，横軸は「製品仕込量」を示します。

• 製品仕込量： ~2000 [kg]
• 製品の比熱： 1 [kcal/kg℃]
• 製品温度： 80 [℃] → 30 [℃]
• 総括伝熱係数： 260 [kcal/m²h℃]
• 冷却水入口温度： 12 [℃]
• 冷却水量： 1000 ~ 12000 [kg/h]

「スケールアップ理論を考えてみよう ー 乳化編【スケールアップによる製造規模の変更】」のページで紹介したように，スケールアップは製造規模の10倍ずつが基本です。

そこで，製品仕込量が10倍になったときの冷却時間を考えてみましょう。

スケールアップ前の仕込量をどこにするかにもよりますが，製品仕込量Mを10倍にスケールアップすると，ジャケット冷却のみの場合，冷却時間θは理論上2倍以上長くなることがわかります。

したがって，スケールアップ前の条件で”急冷”が最適と決めてしまうと，大型の乳化撹拌装置では再現できないことになります。

乳化撹拌装置を使用したジャケット冷却では，いろいろと留意点が出てきそうです。