“単位体積あたりの槽壁伝熱量一定”の一般式としての表し方

「撹拌をやさしく捉えてみよう【撹拌による槽内の流動】」のページで撹拌レイノルズ数を紹介しました。

ここでは，撹拌レイノルズ数が一定のとき，撹拌作用がどのように変化するかを考えてみます。

当社では撹拌レイノルズ数をあまり取り上げて使用することはないので，おまけのようなページとなります。

ご参考までに紹介しますので，読み飛ばしても問題ありません。

一般的に，「N₂/N₁ = (D₂/D₁)^–2」と表されることがあります。

下図に記載されているような計算をすることによって，最終的にこのような結論が得られます。

スケールアップ前

このときの回転数N₁，パドルミキサーの直径D₁とすると，撹拌レイノルズ数は「Re₁= N₁D₁²ρ/60η」となります。

スケールアップ後

このときの回転数N₂，パドルミキサーの直径D₂とすると，撹拌レイノルズ数は「Re₂ = Re₁ ⇔ N₂D₂²ρ/60η」となります。

“撹拌レイノルズ数一定”であるため，「Re₂ = Re₁」となります。

そして，式変形をしていくと「N₂ = N₁(D₁/D₂)²」となります。

回転数Nを左辺，パドルミキサーの直径Dを右辺に移項すると「N₂/N₁ = (D₂/D₁)^–2」が得られます。

📝[memo]　Re₂ = Re₁　⇔　N₂D₂²ρ/60η = N₁D₁²ρ/60η　⇔　N₂D₂² = N₁D₁²　⇔　N₂ = N₁(D₁/D₂)²　⇔　N₂/N₁ = (D₂/D₁)^–2

撹拌レイノルズ数一定時における撹拌作用の関係

“微細化作用He”と“吐出作用Q”を回転数Nとパドルミキサーの直径Dで表現することを考えます。

「スケールアップ理論を考えてみようー乳化編【周先端速度一定時における撹拌作用の変化】」のページで紹介したように，微細化作用Heと吐出量Qは次のように表されます。

• He ∝ N²D²
• Q ∝ ND³

単位体積あたりの撹拌レイノルズ数が一定のとき，これらの撹拌作用がどのように変化するでしょうか？

📝[memo]　伝熱量を考えると撹拌レイノルズ数は必ずしも必要とは限りませんが，参考までに計算したいと思います。

微細化作用の関係

「スケールアップ理論を考えてみよう ー 乳化編【“N^3D^2”とは？】」のページで，スケールアップ後の回転数N₂ = N₁(D₁/D₂)^2/3で表されると紹介しました。

ここで，スケールアップ前後の微細化作用Heを計算します。

• スケールアップ前　👉　He₁ ∝ N₁²D₁²
• スケールアップ後　👉　He₂ ∝ N₂²D₂² = {N₁(D₁/D₂)²}²D₂² = N₁²D₁⁴/D₂²

He₂/He₁ ∝ (N₁²D₁⁴/D₂²)/N₁²D₁² = (D₂/D₁)^–2

したがって，パドルミキサーの直径Dが2倍になると，微細化作用Heは0.25倍になることがわかります。

📝[memo]　パドルミキサーの直径Dの変化の仕方（スケールアップの仕方）によって，微細化作用Heは異なります（＝一定ではありません）。

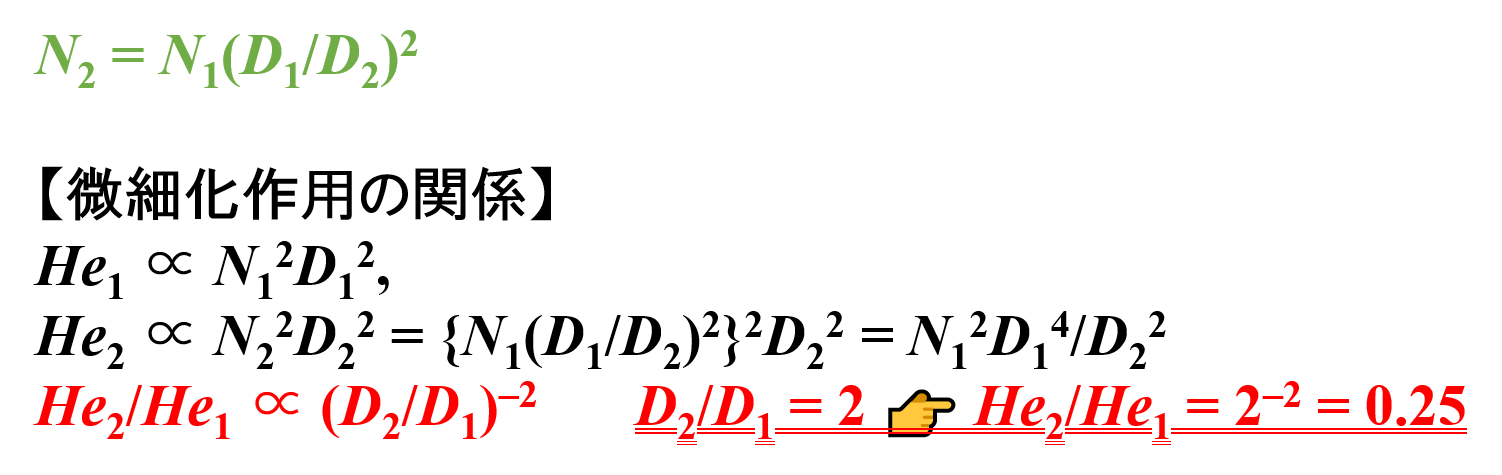
吐出作用の関係

次に，スケールアップ前後の吐出作用Qを計算します。

スケールアップ前　👉　Q₁ ∝ N₁D₁³
スケールアップ後　👉　Q₂ ∝ N₂D₂³ = {N₁(D₁/D₂)²}D₂³ = N₁D₁²D₂

Q₂/Q₁ ∝ N₁D₁²D₂/N₁D₁³ = D₂/D₁

したがって，パドルミキサーの直径Dが2倍になると，吐出作用Qは2倍になることがわかります。

📝[memo]　パドルミキサーの直径Dの変化の仕方（スケールアップの仕方）によって，吐出作用Qは異なります（＝一定ではありません）。

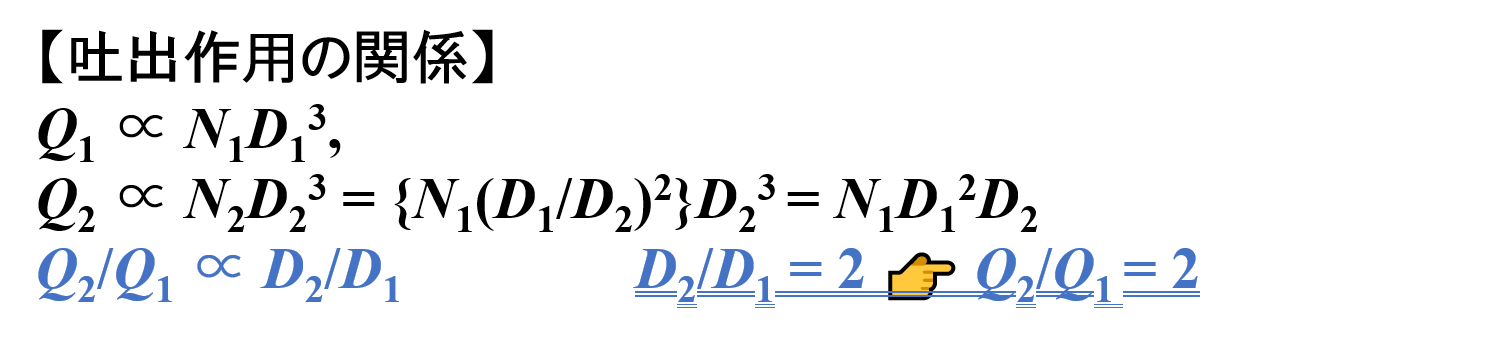
撹拌時間の関係

最後に，「”（条件②）パス回数が等しくなるようにする”という考え方」を採用して，撹拌作用ではありませんが撹拌時間についても考えます。

スケールアップ前　👉　t₁ ∝ n₁V₁/Q₁ ∝ n₁(αD₁³)/(N₁D₁³) = αn₁/N₁

スケールアップ後　👉　t₂ ∝ n₂V₂/Q₂ ∝ n₁(αD₂³)/(N₁D₁²D₂) = αn₁/N₁・(D₂/D₁)²

📝[memo]　パス回数の式を変形した乳化時間t = …の式に，上述した吐出量（吐出作用）Qを代入しています。

📝[memo]　ここでは「パス回数＝循環回数」，「乳化時間＝撹拌時間」と置き換えます。

t₂/t₁ ∝ {αn₁/N₁・(D₂/D₁)²}/(αn₁/N₁) = (D₂/D₁)²

したがって，パドルミキサーの直径Dが2倍になると，撹拌時間tは4倍になることがわかります。

---

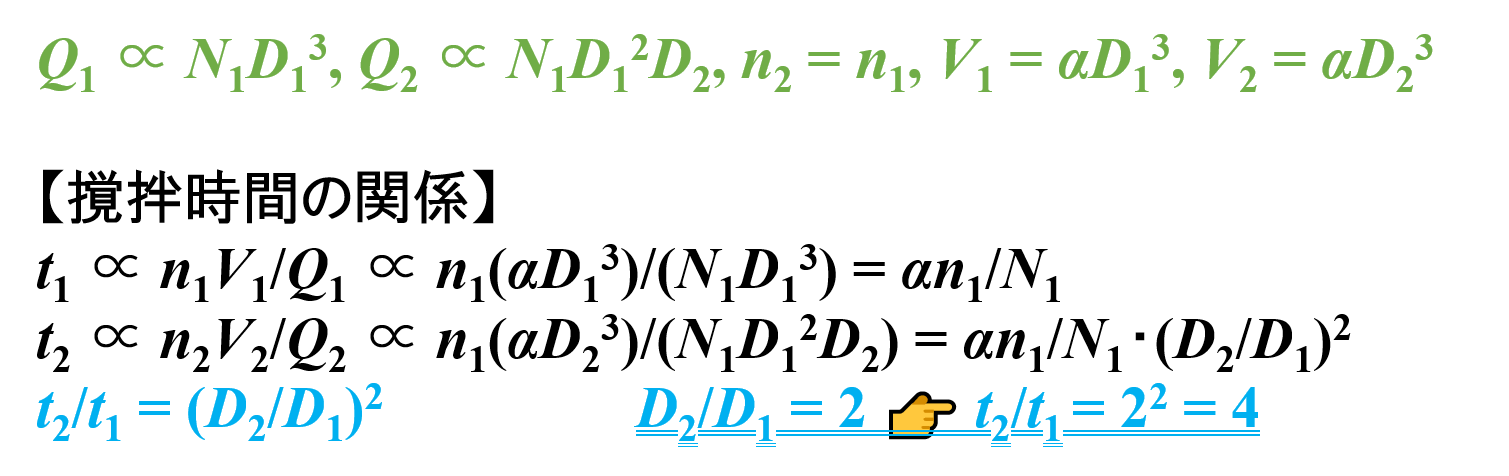
一方，「スケールアップ理論を考えてみよう ー 乳化編【回転数・混合時間/乳化時間の考え方】」のページで紹介した”無次元混合時間”を採用する場合があります。

• スケールアップ前　👉　t_M1 ∝ 1/N₁
• スケールアップ後　👉　t_M2 ∝ 1/N₂ = 1/{N₁(D₁/D₂)²}

📝[memo]　無次元混合時間の式を変形した混合時間t_M = …の式に，上述した回転数Nを代入しています。

📝[memo]　ここでは「撹拌時間＝混合時間」と置き換えます。

t_M2/t_M1 ∝ [1/{N₁(D₁/D₂)²}]/(1/N₁) = (D₂/D₁)²

したがって，パドルミキサーの直径Dが2倍になると，混合時間t_Mは4倍になることがわかります。

📝[memo]　循環回数（パス回数）で考えた場合と同じ式が得られ，混合時間t_Mはパドルミキサーの直径Dだけで表すことができます。

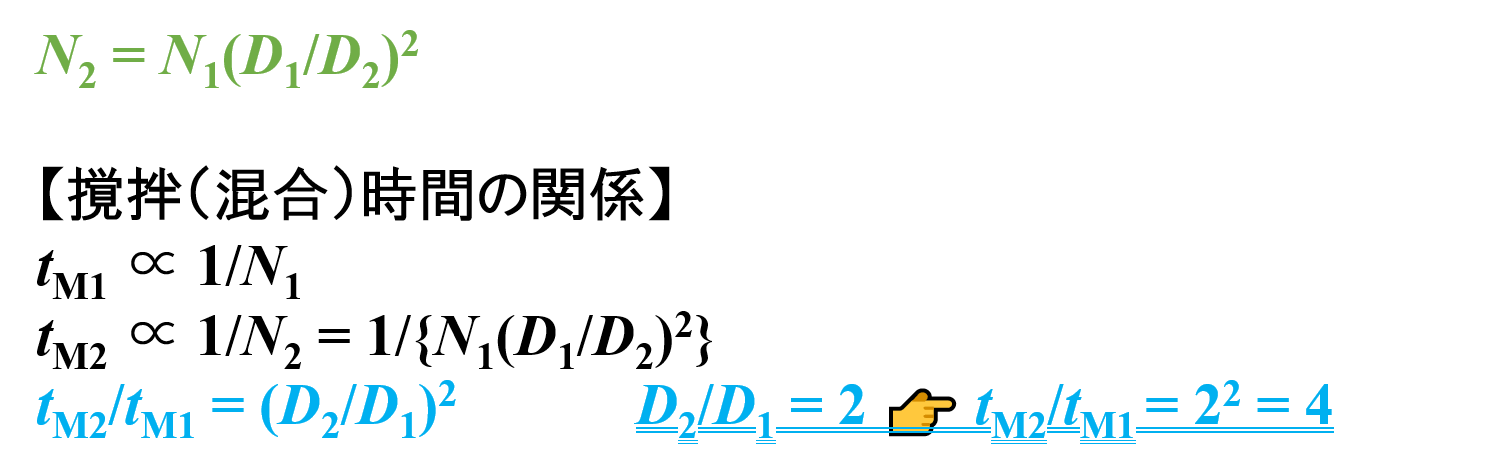
まとめ

ここで，まとめをしておきましょう。

スケールアップをして羽根径が2倍になると，単位体積あたりの動力一定時において各種因子は下表のように変化します。

---

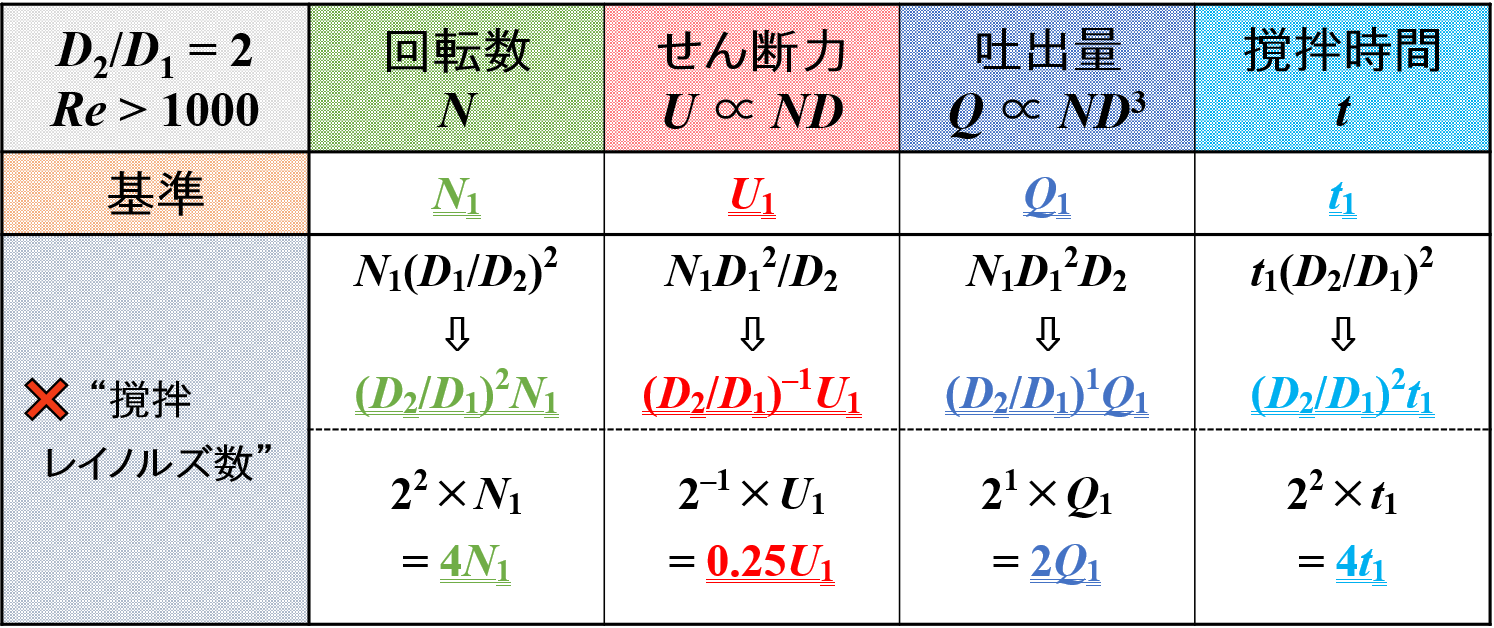
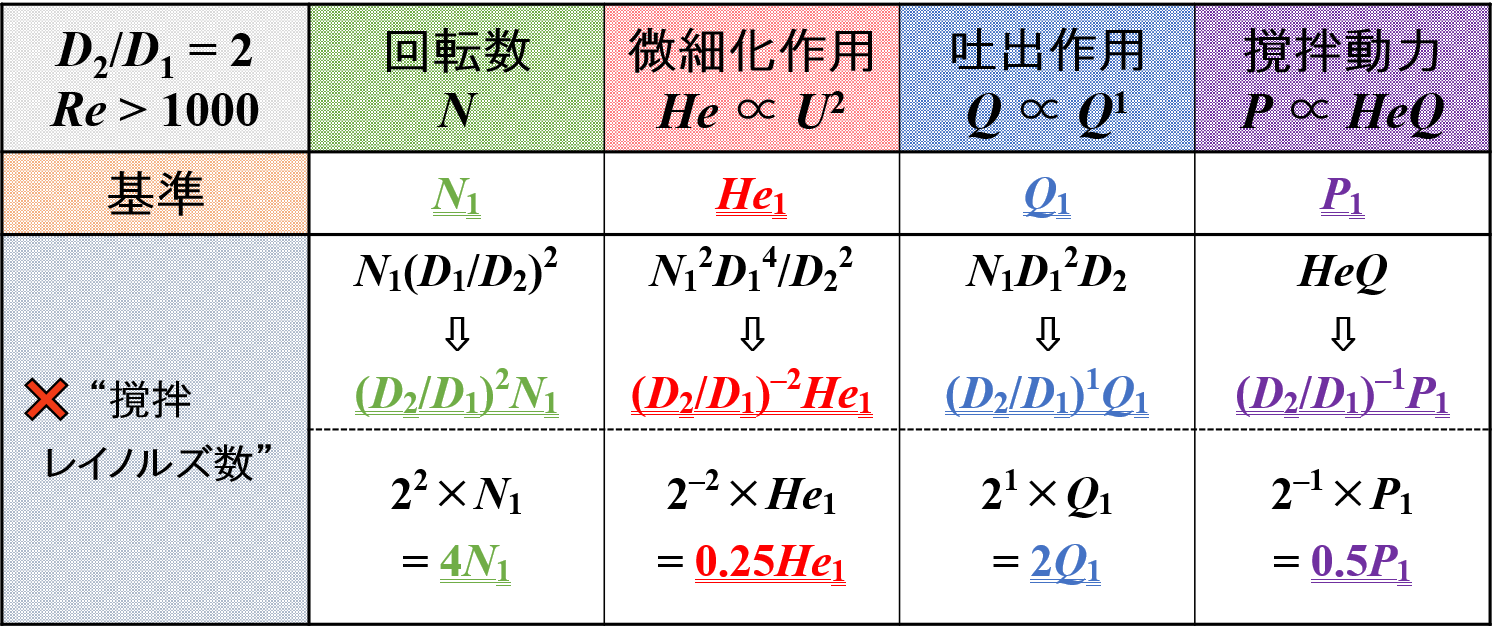
撹拌レイノルズ数一定とするスケールアップは，こんな感じの変化をするんだな！位の感想で充分です。

色々なスケールアップ手法があるので，一つの事例として紹介しました。

冷却速度一定の考え方まとめ

おまけの話が続きましたが，ここでメインの話に戻しましょう。

これまでに冷却速度一定について考えてきたので，論点をまとめておきましょう。

「スケールアップ理論を考えてみよう ー 乳化編【相似則の利用】」のページで紹介したように，機械的な力を等しくするために“相似則”の関係を採用することを考えるのが基本でした。

そこで，「スケールアップ理論を考えてみよう ー 冷却編【冷却速度一定とする考え方①】」のページで幾何学的相似を満たすように乳化槽の伝熱面積Aや製品仕込量Vを考えましたが，上手くいかないことがわかりました。

続いて，「スケールアップ理論を考えてみよう ー 冷却編【単位体積あたりの槽壁伝熱量一定時における撹拌作用の変化】」のページで力学・運動学的相似を満たすように単位体積あたりの槽壁伝熱量を一定にすることを考えました。

理論式を確認してみると，実際に適用することは難しそうです。

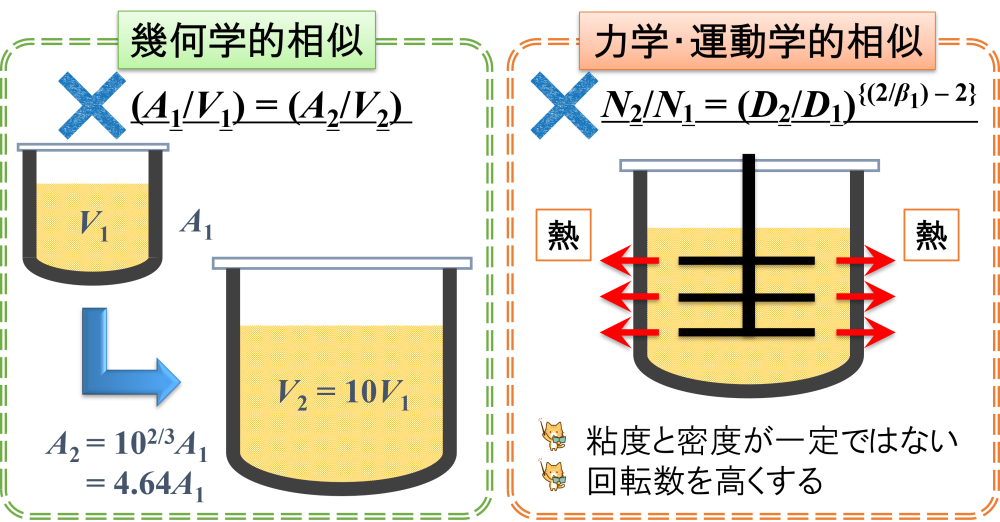
したがって，幾何学的相似と力学・運動学的相似のいずれも満たすことができないという結論が得られます。

これは，スケールアップ前後で冷却速度を一定にすることができないことを意味します。

…ということで，冷却速度一定を目指すことを諦め，冷却速度向上に向けた検討を試みることになります。