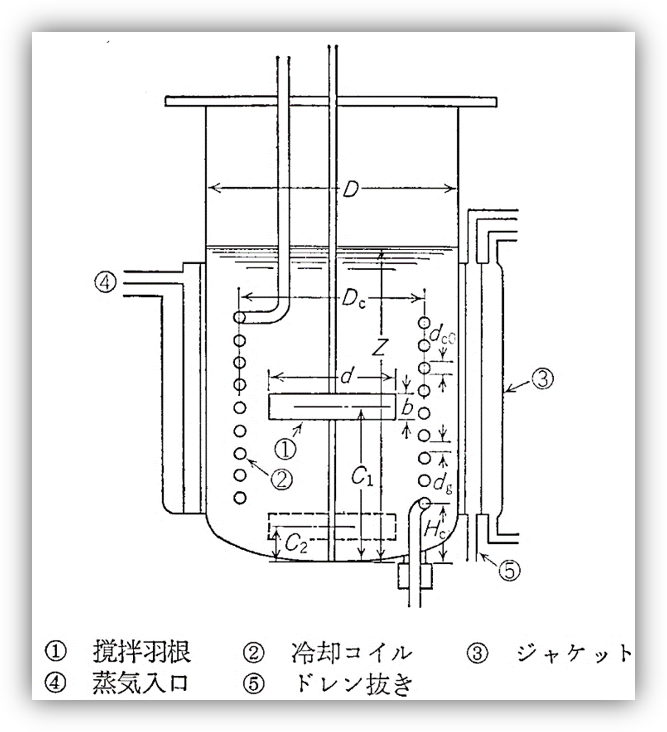
📚 (6-2) スケールアップ理論を考えてみよう ー 冷却編【冷却速度一定とする考え方①】
- #乳化撹拌装置
- #乳化
- #エマルション
- #スケールアップ

冷却を制御する幾何学的相似条件
「スケールアップ理論を考えてみよう ー 冷却編【冷却モデル】」のページでは,冷却速度に関して2つの考え方を紹介しました。
最初に,スケールアップ前後で冷却速度を一定にすることを目指してみたいと思います。
単位体積あたりの槽壁伝熱量

”単位体積あたりの冷却速度”を”単位体積あたりの槽壁伝熱量qV”と呼びたいと思います。
単位体積あたりの槽壁伝熱量qVは,「単位時間あたりの伝熱量q/製品仕込量V」で表すことができます。
まずは,式の形から考えてみたいと思います。

「スケールアップ理論を考えてみよう ー 冷却編【冷却モデル】」のページで紹介したように,製品中の熱は”乳化物 → 伝熱境膜 → 乳化槽 → 冷却水”の順に移動すると考えることにしました。
ここでは一纏めにした伝熱係数を考えることにして,これを総括伝熱係数Uと定義することにします。
📝[memo] 乳化撹拌装置における乳化槽を使用するときは,総括伝熱係数Uは一定であるとして考えます。

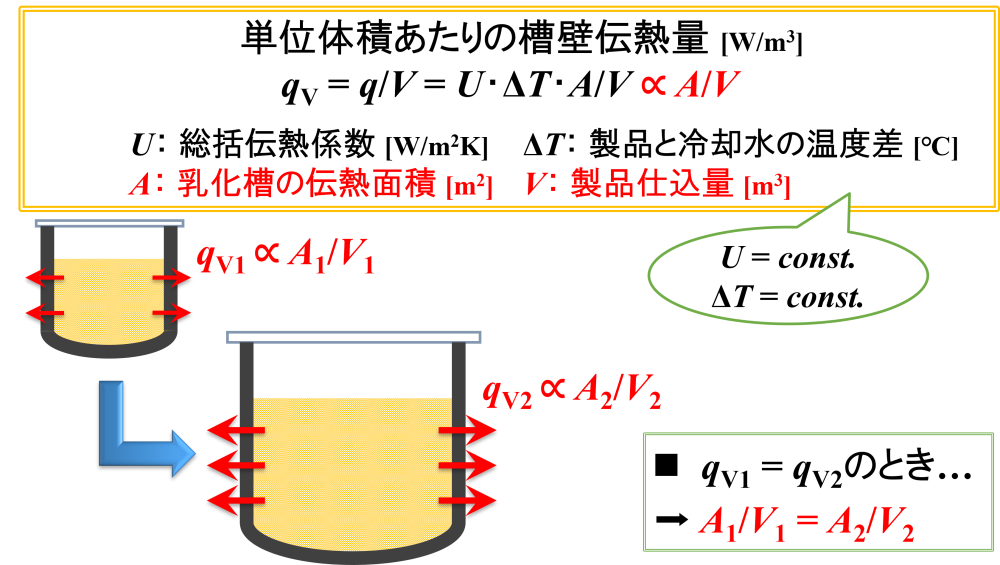
単位体積あたりの槽壁伝熱量qVは,総括伝熱係数U,製品と冷却水の温度差ΔT,乳化槽の「伝熱面積A/製品仕込量V」に比例します。
冷却条件を等しくしてスケールアップするので,製品と冷却水の温度差ΔTは一定になります。
すると,単位体積あたりの伝熱量qVは乳化槽の「伝熱面積A/製品仕込量V」のみに比例することがわかります。
すなわち,「伝熱面積A/製品仕込量V」を一定にすることができれば,単位体積あたりの槽壁伝熱量qVを等しくするというスケールアップができることを意味します。
このとき,「伝熱面積A/製品仕込量V」は乳化槽の形状に起因する条件であるため,単位時間あたりの伝熱量は”力学・運動学的相似条件”を適用すべきかもしれませんが,結果的に”幾何学的相似条件”として考えたいと思います。
📝[memo] 「スケールアップ理論を考えてみよう ー 乳化編【相似則の利用】」のページで紹介したように,機械的な力を等しくするために“相似則”の関係を採用することを考えるのが基本でした。

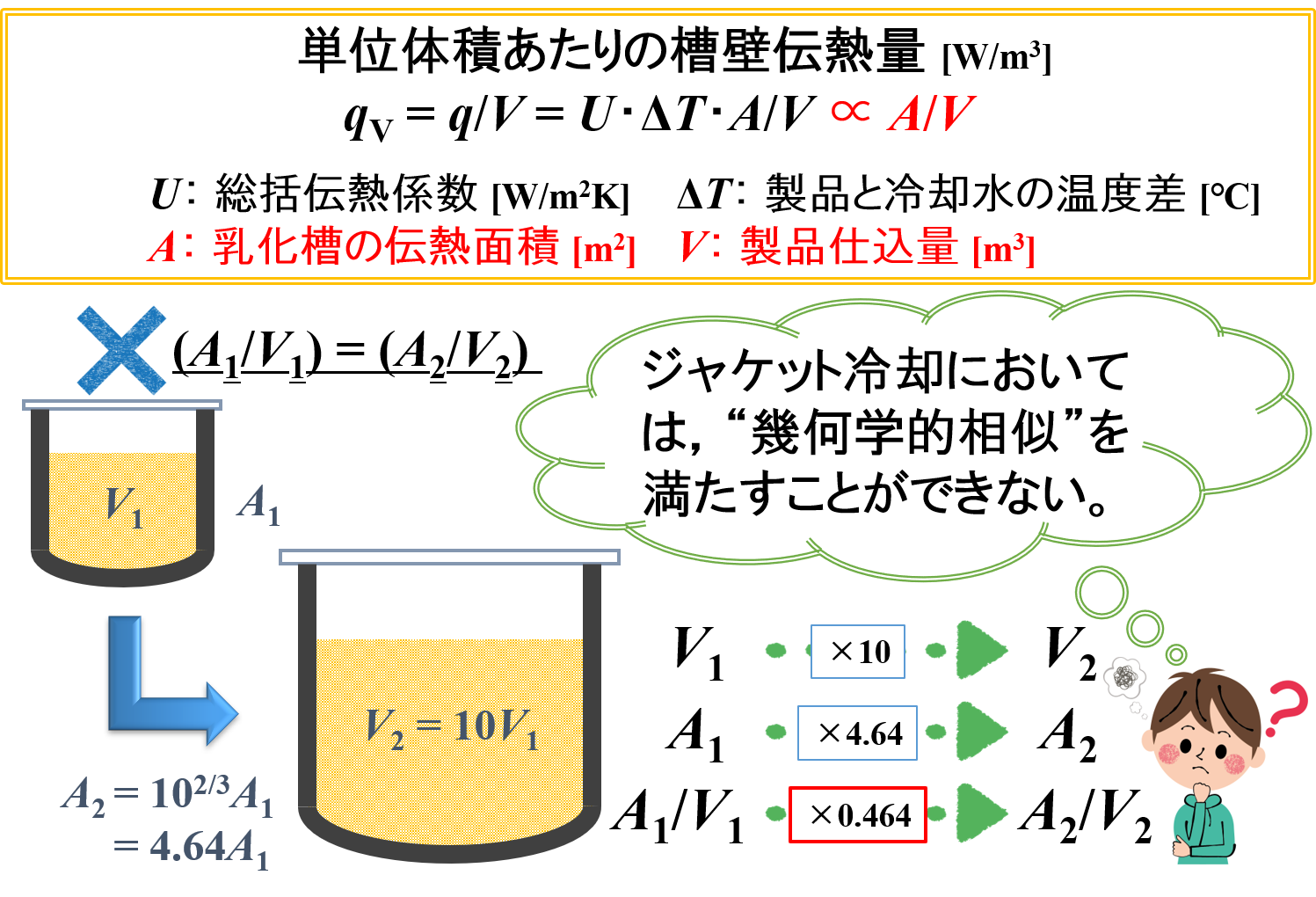
例えば,10倍にスケールアップ(製品仕込量Vが10倍)した事例を考えます。
このとき,乳化槽の伝熱面積Aは10倍にはならず,約4.64倍(= 102/3倍)にしかなりません。
すなわち,「伝熱面積A/製品仕込量V」を一定にすることはできません。
その結果,スケールアップ前後で単位体積あたりの槽壁伝熱量qVに0.464倍(= 10-1/3倍)の差異が生じていることがわかります。
📝[memo] qV2 = q2/V2 = 102/3q1/10V1 = 10-1/3q1/V1 = 10-1/3qV1

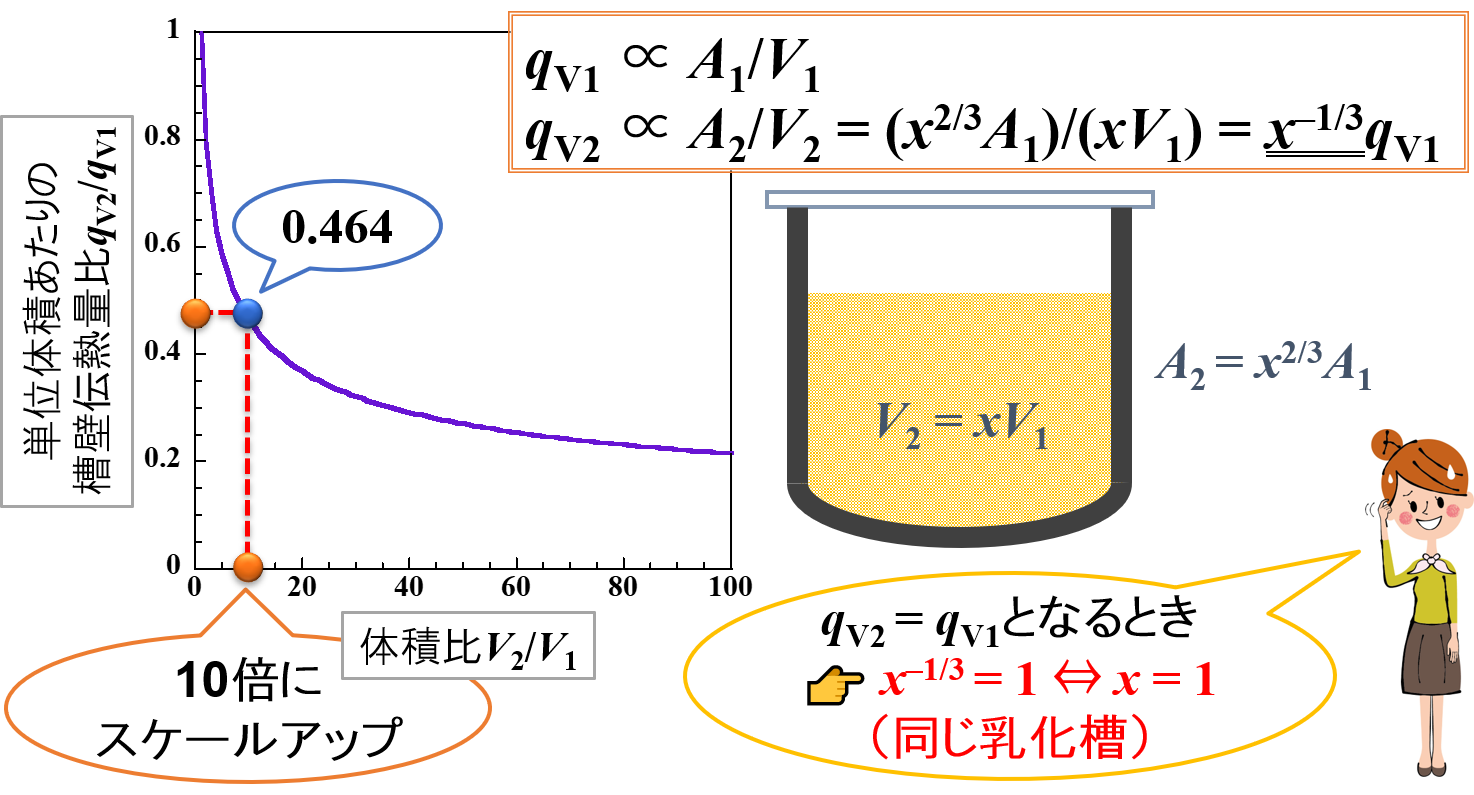
例えば,x倍にスケールアップしたとして計算をしてみると,「qV2 = x-1/3qV1」の関係式が得られます。
「伝熱面積A/製品仕込量V」を一定にする条件を満たすためには,x = 1(1倍にスケールアップ=同じ乳化槽)のときになります。
📝[memo] x = 1以外の解が見つかりません。
したがって,幾何学的相似を満たすことで,冷却速度(単位体積あたりの槽壁伝熱量qV)を一定にすることは困難であるという結論が得られます。
乳化槽壁面からの距離
別の視点からも考えたいと思います。
10倍にスケールアップ(製品仕込量Vが10倍)したとき,乳化槽径Rは約2.15倍(= 101/3倍)だけ長くなります。
これがどのような意味を持つかというと,乳化槽壁面と乳化物(エマルション)間の距離が長くなるということです。
すなわち,乳化槽壁面に近い乳化物は優先的に冷却されますが,これより遠い乳化物はなかなか冷却されません。
その結果,乳化物の同時に温度差(温度ムラ)が大きくなってしまいます。
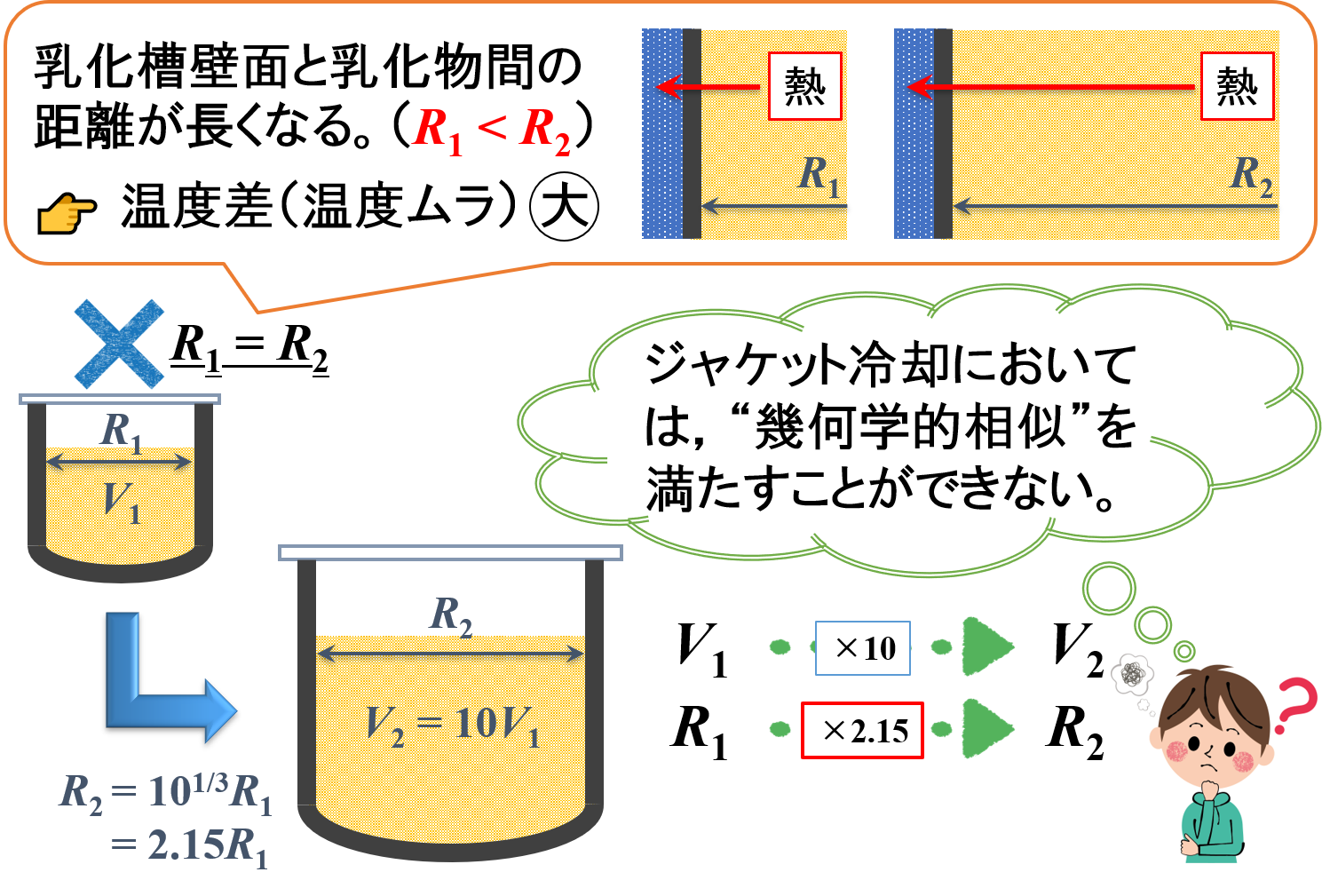
それではどうしたら良いかというと,乳化槽径Rを等しくすることを考えます。
しかしながら,スケールアップをしている以上,乳化槽径Rが等しくなることはあり得ません。
📝[memo] スケールアップでは,大きな乳化槽を使用することが大前提です。
先述したように,冷却速度(単位体積あたりの槽壁伝熱量qV)を一定にすることは困難であるという結論が得られましたが,同時に温度差(温度ムラ)が生じやすくなるという問題が出てきます。
改めて,幾何学的相似を満たすことは難しいことがわかります。
ジャケット冷却とコイル冷却

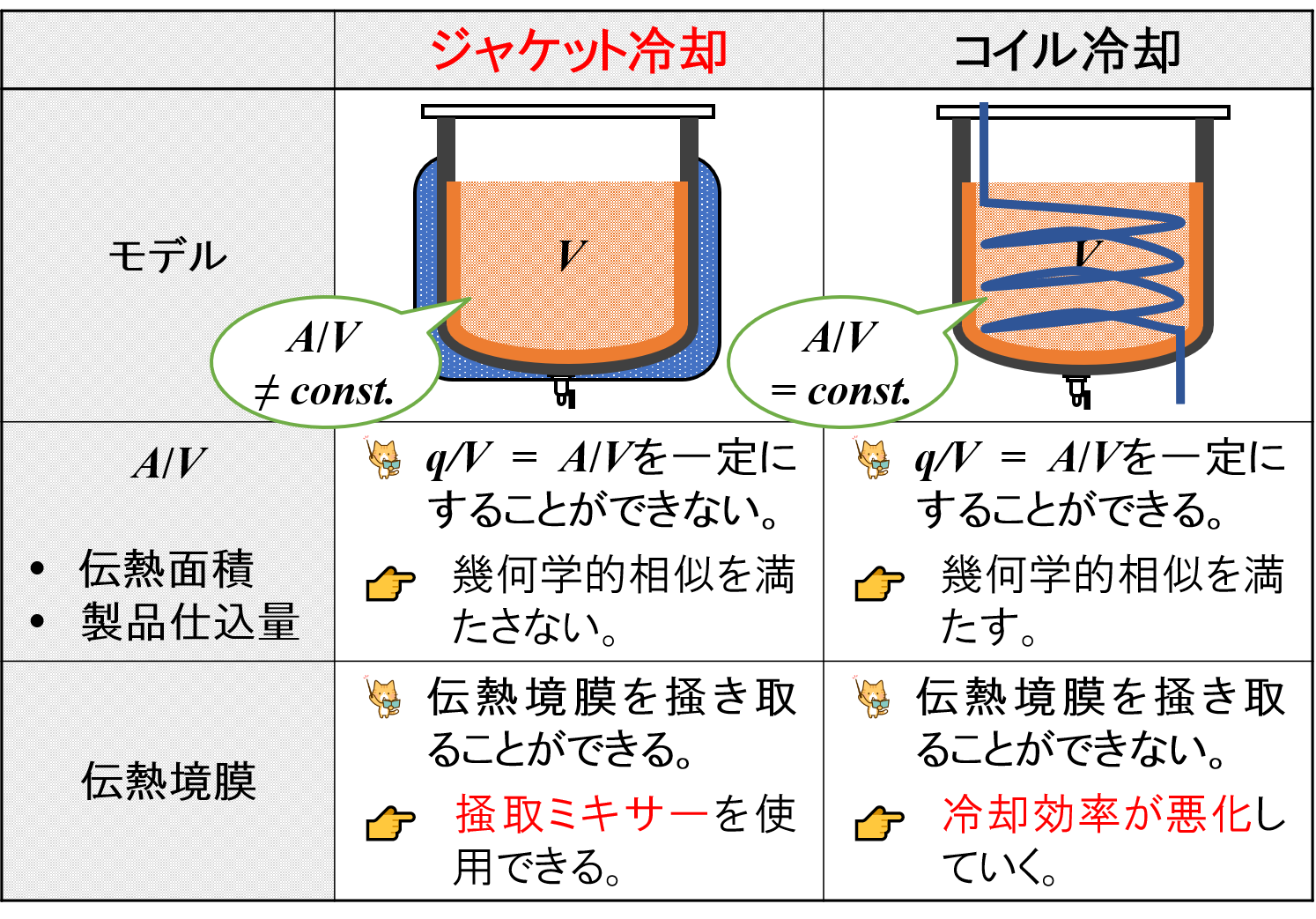
ジャケット冷却では,乳化槽の伝熱面積Aや製品仕込量Vのバランスが崩れるのでスケールアップが上手くできませんでした。
そこで,乳化槽の伝熱面積Aに相当する部分を大きくすることで,スケールアップが上手くできるように工夫することができます。
その手段の一つとして,コイル冷却があります。

一方で,「スケールアップ理論を考えてみよう ー 冷却編【冷却モデル】」のページで紹介したように,エマルション製品は冷却するにつれて増粘していく傾向が見られます。
すると,乳化槽壁面やコイル表面に伝熱境膜が生成します。
乳化槽の場合は掻取ミキサーを使用してこのような伝熱境膜を掻き取ることができますが,コイル冷却の場合は伝熱境膜は残存したままです。
その結果,コイル冷却では冷却効率が悪化していくことが懸念されます。
したがって,エマルション製品の冷却工程ではコイル冷却を採用することはほとんどありません。
製品と冷却水の温度差を変数とするとき
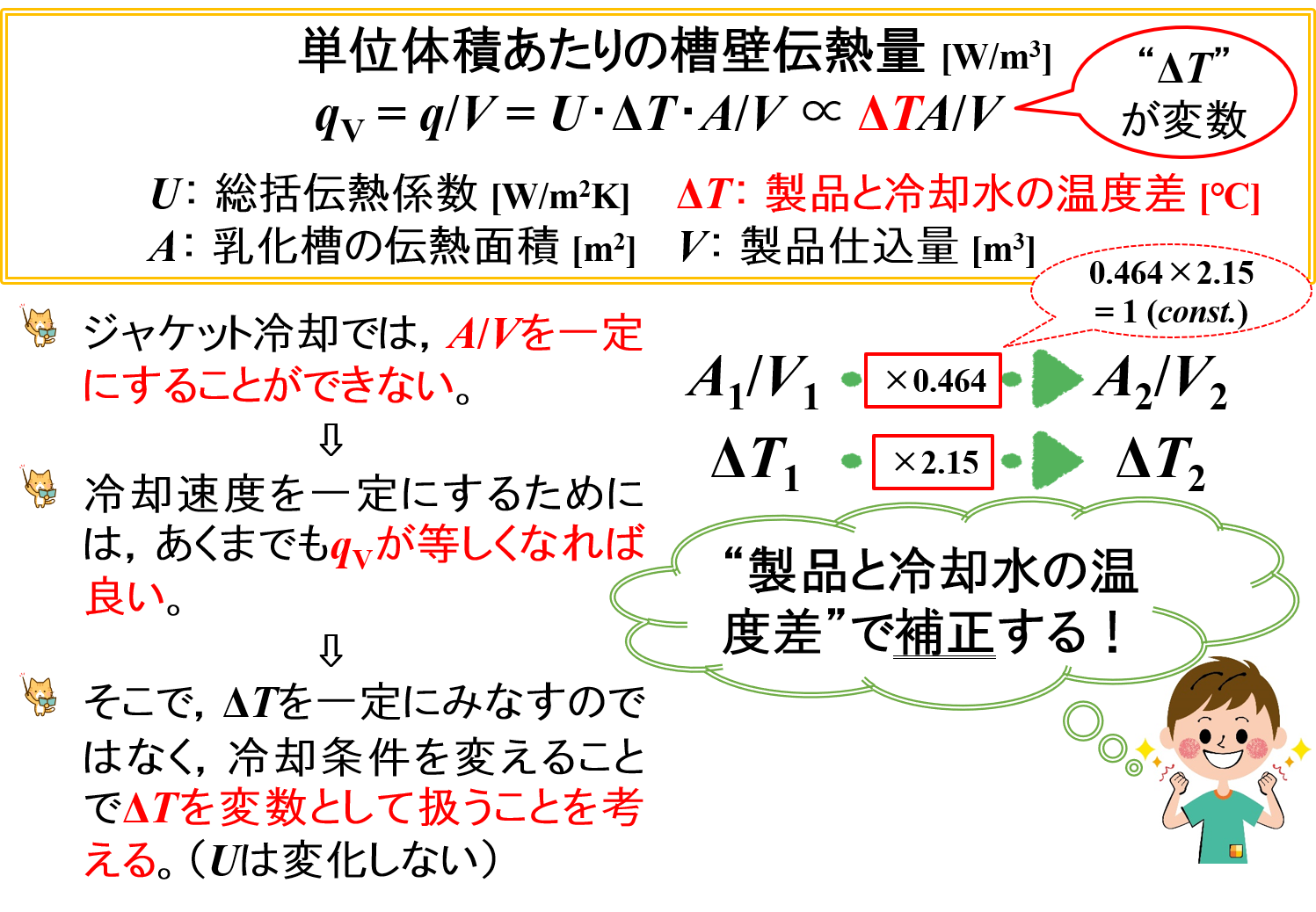
ところで,製品中の熱は”乳化物 → 伝熱境膜 → 乳化槽 → 冷却水”の順に移動するので,総括伝熱係数Uは定数とみなされます。(総括伝熱係数Uは変化しません。)
一方,製品と冷却水の温度差ΔTは冷却条件によって変化します。
したがって,製品と冷却水の温度差ΔTを変化させることで,約0.464倍(= 10-1/3倍)に変化する「伝熱面積A/製品仕込量V」を補正できるかもしれません。
これは,冷却速度を一定にするためには,あくまでもqVが等しくなれば良いという考え方です。
結論を言うと,製品と冷却水の温度差ΔTが約2.15倍(= 101/3倍)にになれば良いことがわかります。
それでは,実務においてこのような対応ができるでしょうか?
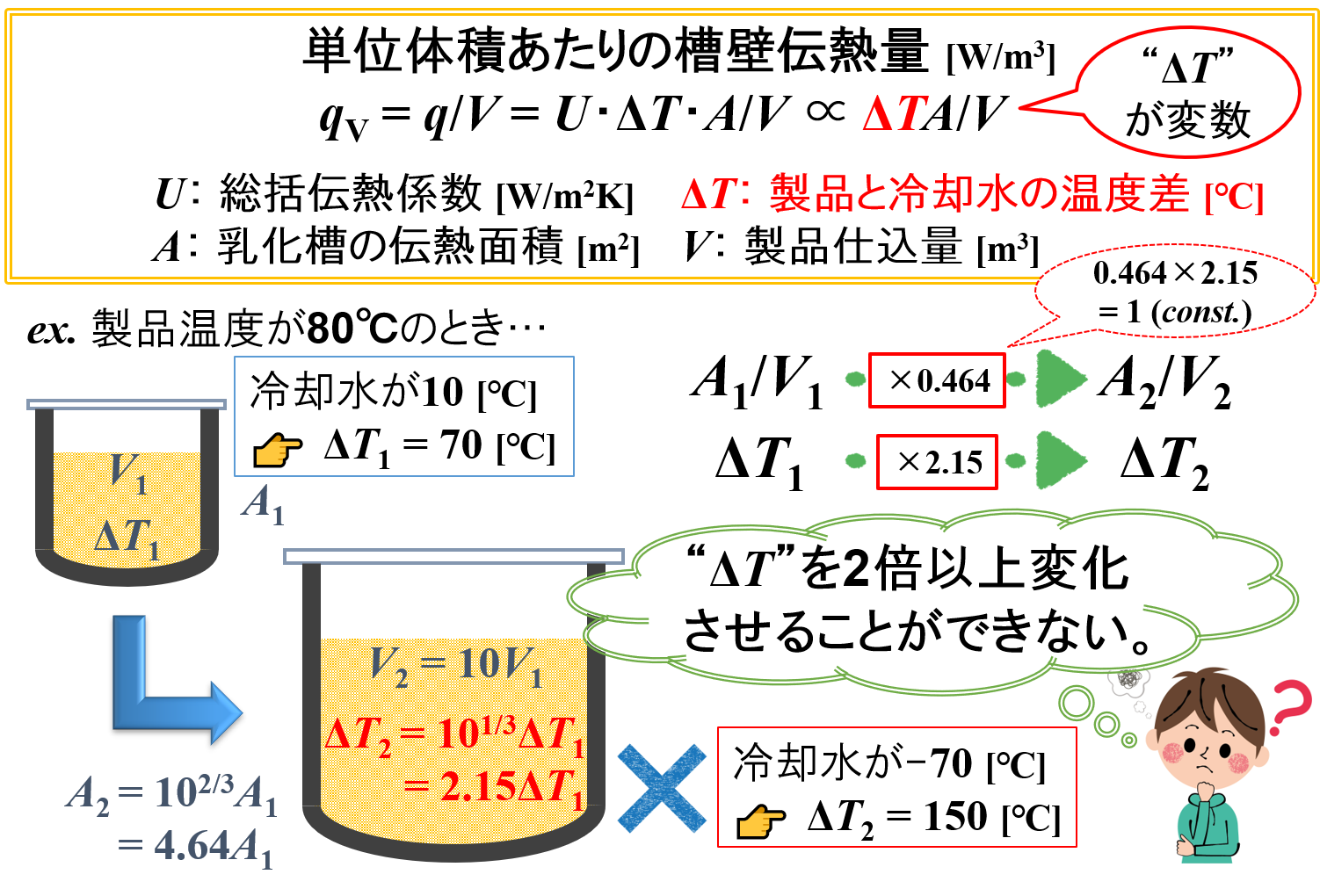
例えば,80℃の製品を冷却することを考えます。
冷却水の温度が10℃のときは,製品と冷却水の温度差ΔTは70℃になります。
10倍にスケールアップしたときは製品と冷却水の温度差ΔTが150℃であることが求められるので,-70℃の冷却水を使用しなければなりません。
このような対応は実際には無理な話なので、製品と冷却水の温度差ΔTを変化させるという考え方は採用できません。
冷却を制御するための計算(推算)式
そこで,力学・運動学的相似条件を考えることになります。
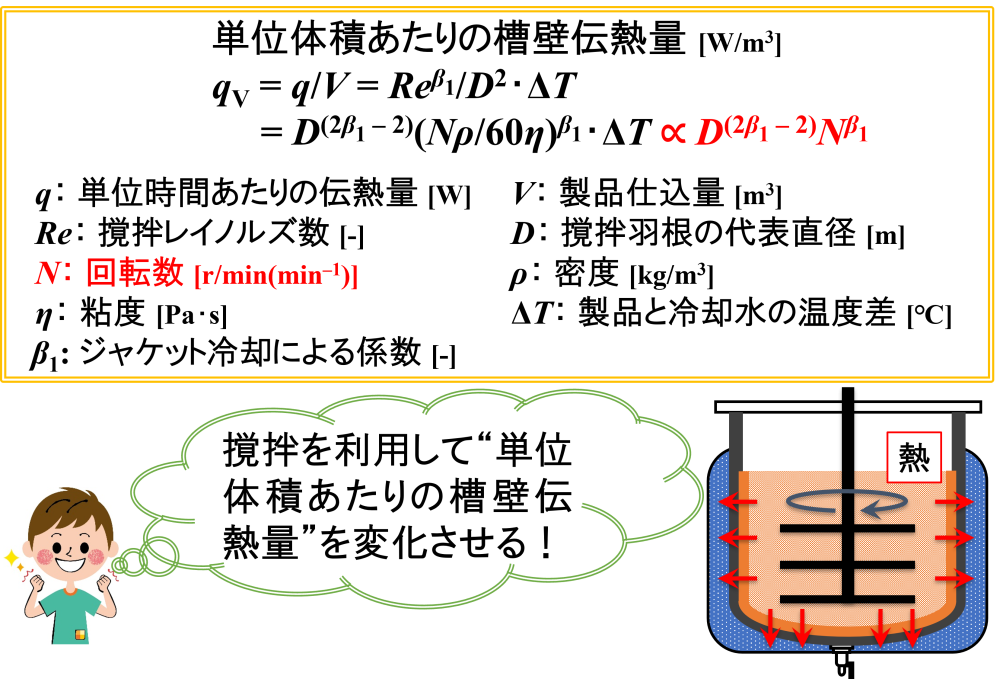
このとき登場するのが”冷却を制御するための計算(推算)式”=”単位体積あたりの槽壁伝熱量の式”です。
これは,撹拌によって製品を流動させ,“単位体積あたりの槽壁伝熱量”を変化させるものです。
回転数Nが決まれば,単位体積あたりの槽壁伝熱量qVが算出できそうです。
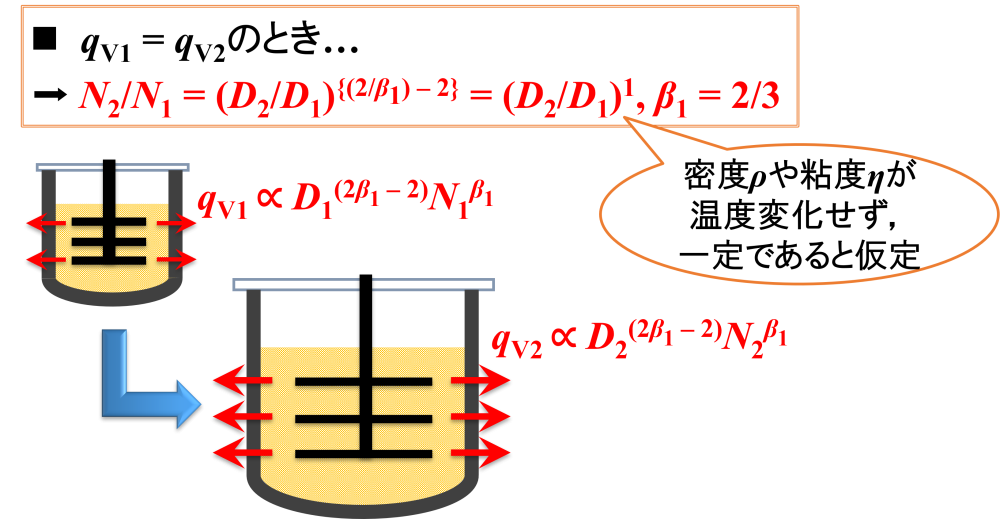
問題点

しかしながら,この式を使用するにあたって問題点があります。
冷却時において,温度によってエマルション製品の密度ρや粘度ηが連続的に変化します。
そのため,密度ρや粘度ηが定数として決まらないため,単位体積あたりの槽壁伝熱量qVが一定とは限りません。
したがって,単位体積あたりの槽壁伝熱量qVを一定とする(=冷却速度を一定とする)条件を算出することは困難であるという結論が得られます。
一方で,回転数Nの問題もあります。
「スケールアップ理論を考えてみよう ー 冷却編【冷却速度一定とする考え方②】」のページで改めて紹介しますが,スケールアップ理論と実際がかけ離れているという事実が判明します。
したがって,”単位体積あたりの槽壁伝熱量の式”が使用できないという結論になります。
単位体積あたりの槽壁伝熱量の式の導出
ご参考までに,単位体積あたりの槽壁伝熱量の式の導出したいと思います。
ひたすら式変形が続くので,読み飛ばしても問題ありません。
🚩 [引用:社団法人化学工学協会編『化学工学便覧』丸善,1988]

永田の式
hD/λ = α(Cpη/λ)1/3(η/ηw)0.14Reβ1×(d/D)β2(ΣCi/iz)β3(Σbi/D)β4×npβ5(sinθ)β6(Z/D)β7
⇔ h ∝ Reβ1/D …(1)
インデックスの詳細は明記していませんが,スケールアップ前後で変化しない定数を無視すると上記の式が得られます。

伝熱面積
A = kD2 …(2)
面積は長さの2乗に比例します。(kは比例定数)

掻取ミキサーの直径
d = D …(3)
掻取ミキサーの羽根径=乳化槽径として,ホームページの表記に合わせます。

全伝熱量
q = h・ΔT・A …(4)
伝熱係数hを使用した単位時間あたりの伝熱量を示しています。
式(1), (2), (3)を式(4)に代入すると,
q = h・ΔT・A = (Reβ1/D)・ΔT・kD2 ∝ Reβ1・ΔT・D …(5)
製品仕込量
V = sD3 …(6)
体積は長さの3乗に比例します。(sは比例定数)

単位体積あたりの槽壁伝熱量
qV = q/V = Reβ1・ΔT・D/sD3 ∝ Reβ1・ΔT/D2 = (D2Nρ/60η)β1・ΔT/D2 = D(2β1 – 2)(Nρ/60η)β1・ΔT
式(5)÷式(6)より算出します。