撹拌作用の変化

これまで，スケールアップ理論を考えるにあたって様々な条件で検討をしてきました。

一旦，整理をしておきましょう。

• せん断力一定　👉　スケールアップ理論を考えてみよう ー 乳化編【周先端速度一定時における撹拌作用の変化】
• 単位体積あたりの動力一定　👉　スケールアップ理論を考えてみよう ー 乳化編【単位体積あたりの動力一定時における撹拌作用の変化】
• 単位体積あたりの吐出量一定　👉　スケールアップ理論を考えてみよう ー 乳化編【単位体積あたりの吐出量一定時における撹拌作用の変化】
• 吐出量一定　👉　スケールアップ理論を考えてみよう ー 乳化編【吐出量一定時における撹拌作用の変化】

撹拌作用として微細化作用と吐出作用が挙げられますが，スケールアップ前後でこれらの撹拌作用を一定にすることで，付与する機械的な力を等しくすることができるという考え方がありました。

「撹拌をやさしく捉えてみよう【撹拌作用の使い分け】」のページで紹介したように，撹拌エネルギーPは微細化作用Heと吐出作用Qの積に比例します。

ここでは，正味の所要動力P_net ＝ 撹拌エネルギーPとします。

微細化作用Heや吐出作用Qのベースとなる因子を確認できたので，正味の所要動力P_netに当てはめて大きさを考えてみましょう。

すると，微細化作用と吐出作用は下記のように表現できます。

乱流域：P_net = K₁ρN³D⁵ = K₁ρ(ND)²(ND³)¹ ∝ (ND)²(ND³)¹ ∝ HeQ

• 微細化作用He ∝ (ND)² = N²D²
• 吐出作用Q ∝ (ND³)¹ = ND³

層流域：P^*_net = (K₂/Re)ρN³D⁵ = (K₂/Re)ρ(ND)²(ND³)¹ ∝ (1/Re)(ND)²(ND³)¹ ∝ (1/Re)HeQ

📝[memo]　 N_p = K₁ = K₂/Re ⇔ N_pRe = K₂

敢えて撹拌レイノルズ数Reを残して考えると，乱流域と同じ「(ND)²(ND³)¹」の項が登場します。

したがって，乱流域と同じ考え方で良いと思うのですが，撹拌レイノルズ数の項(1/Re)がくっ付いています。

すなわち，層流域では撹拌レイノルズ数の影響を受けて撹拌作用が変化します。

そこで，乱流域よりも小さくなった層流域における微細化作用と吐出作用を考えます。

層流域：P^*_net = K₂ηN²D³ = K₂η(ND)^3/2(ND³)^1/2 ∝ He^3/4Q^1/2 ∝ He^*Q^*

• 微細化作用He^* ∝ (ND)^3/2 = N^3/2D^3/2 (= He^3/4)
• 吐出作用Q^* ∝ (ND³)^1/2 = N^1/2D^3/2 (= Q^1/2)

📝[memo]　層流域についてはこれまで考えてきませんでしたが，後半に少しだけ登場します。

微細化作用と吐出作用が一定になるためのスケールアップ

スケールアップ前後で微細化作用と吐出作用を一定にするためにはどうしたら良いかを考えてみましょう。

📝[memo]　ここでは，一般的な乱流域の場合を想定して考えます。

微細化作用の関係

最初に，スケールアップ前後の微細化作用Heを計算します。

• スケールアップ前　👉　He₁ ∝ N₁²D₁²
• スケールアップ後　👉　He₂ ∝ N₂²D₂²

そして，スケールアップ前後で微細化作用が一定となるためには，He₁ = He₂ ⇔ He₂/He₁ = 1を満たす必要があります。

ここで，N = N₂/N₁，D = D₂/D₁であるとします。

すると，下記の関係式が得られます。

He₂/He₁ ∝ (N₂/N₁)²(D₂/D₁)² = N²D² = 1　…⑴

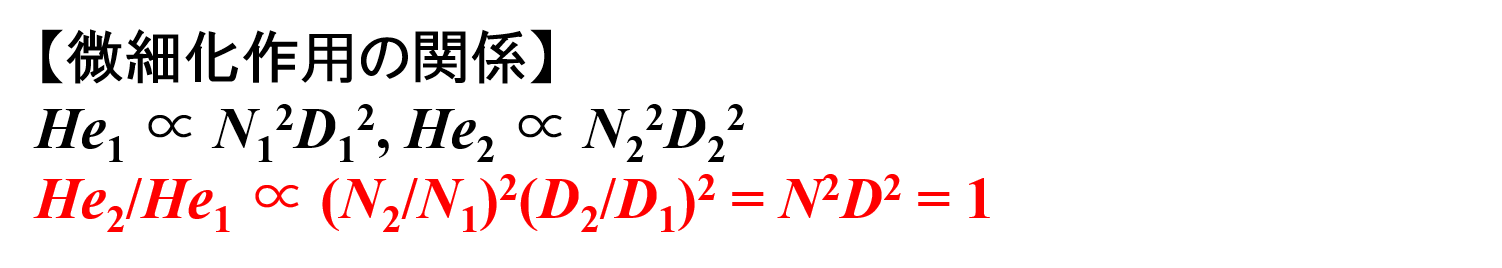
吐出作用の関係

続いて，スケールアップ前後の吐出作用Qを計算します。

スケールアップ前　👉　Q₁ ∝ N₁D₁³
スケールアップ後　👉　Q₂ ∝ N₂D₂³

そして，スケールアップ前後で吐出作用が一定となるためには，Q₁ = Q₂ ⇔ Q₂/Q₁ = 1を満たす必要があります。

すると，下記の関係式が得られます。

Q₂/Q₁ ∝ (N₂/N₁)(D₂/D₁)³ = ND³ = 1 ⇔ N = 1/D³　…⑵

---

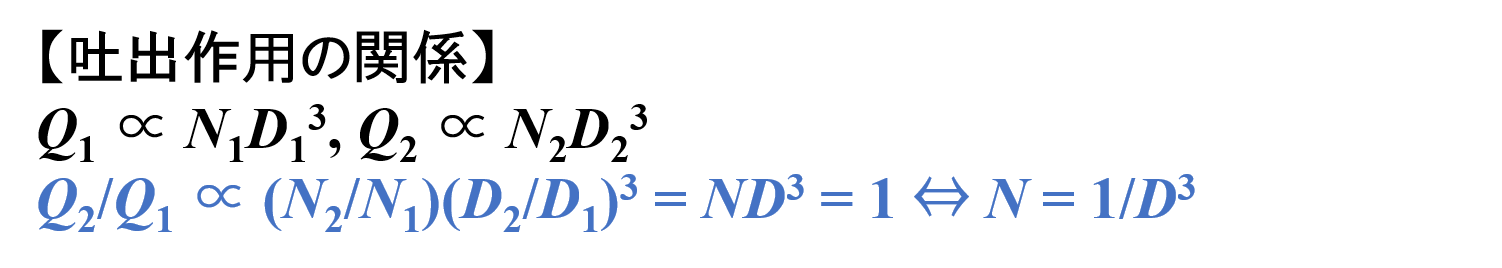
このようにして関係式⑴⑵が得られたので，スケールアップ前後で微細化作用と吐出作用が一定になるための回転数変化Nと羽根径変化Dを求めてみます。

⑵式を⑴式に代入すると，D > 0の条件からD = D₂/D₁ = 1　…⑶を満たさなければならないことがわかります。

次に⑶式を⑵式に代入すると，N = N₂/N₁ = 1　…⑷を満たさなければならないことがわかります。

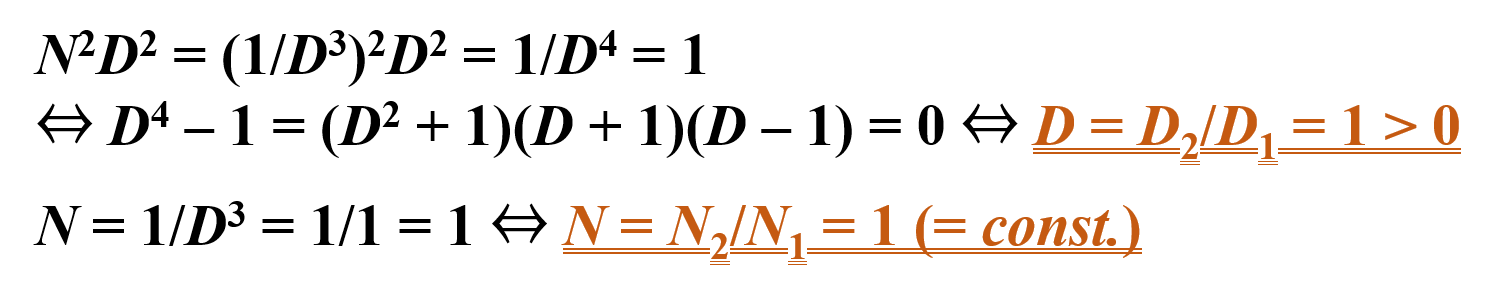
すなわち，微細化作用と吐出作用を共に一定にするためには，回転数と羽根径を変化させてはならない（D = D₂/D₁ = N = N₂/N₁ = 1）という結論が得られます。

しかしながら，スケールアップ前後でこのような条件を守ることは不可能です。

📝[memo]　大型の乳化撹拌装置になると，少なくとも羽根径は大きくなります。

すなわち，スケールアップ時に微細化作用と吐出作用を共に一定にすることができないことがわかりました。

したがって，優先すべき条件は何か？ということを考え，スケールアップを検討しなければなりません。

“羽根径”と各種因子の関係

そこで，優先すべき条件について考えることになるのですが，実際に採用できるのは「せん断力一定」と「単位体積あたりの動力一定」の条件でした。

このとき，スケールアップ後に必要な回転数や微細化作用と吐出作用，撹拌時間（乳化時間）を比較してみましょう。

乱流域

各種因子の変化は，下表のように一般化して表現することができます。

各種因子は，羽根径変化に対して指数関数的に変化します。

ただし，このままだとイメージしにくいので，スケールアップ後に羽根径が2倍になった（D₂/D₁ = 2）と仮定して各種因子の変化を考えることにします。

すると，各種因子の大きさを見積もることができます。

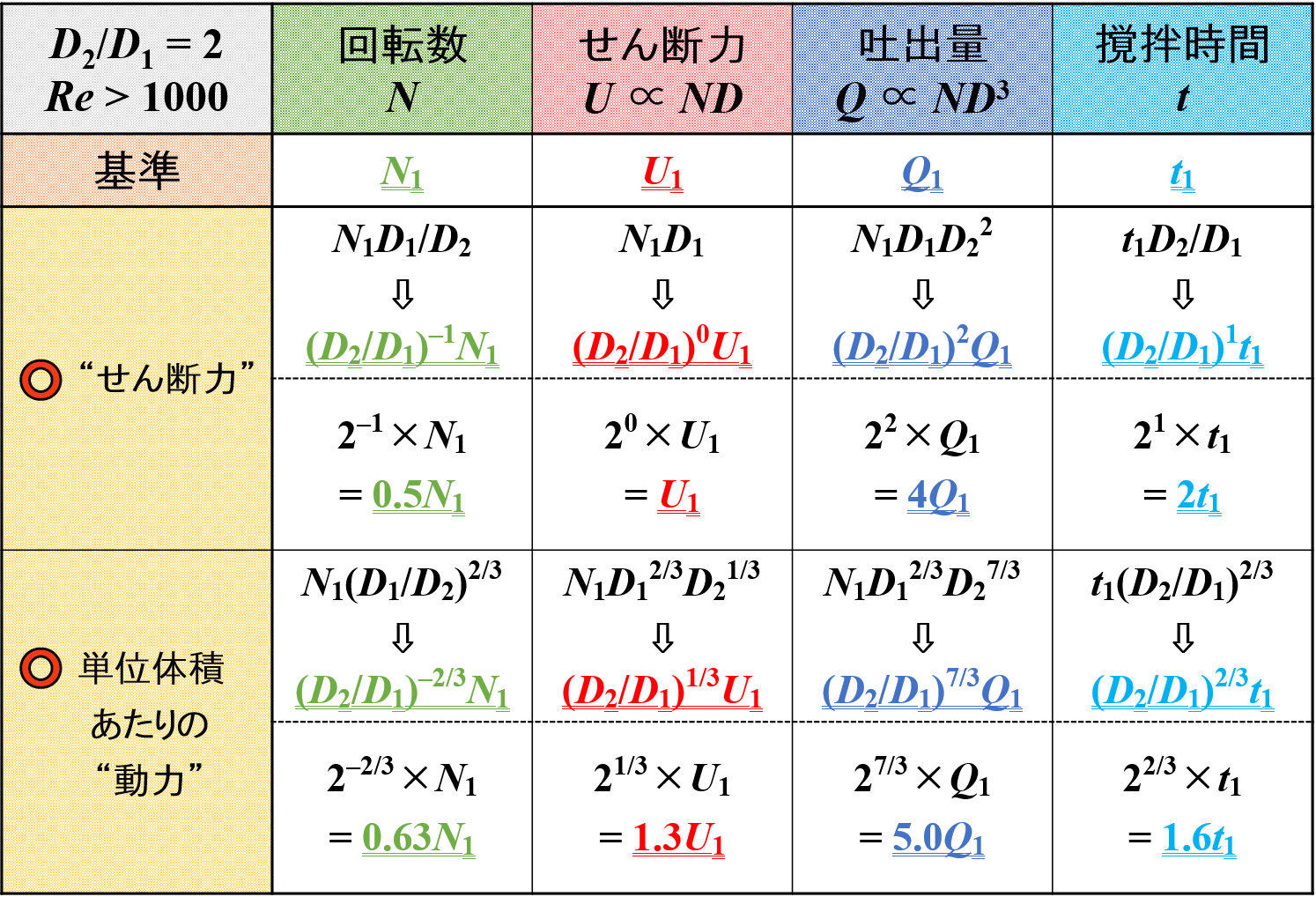
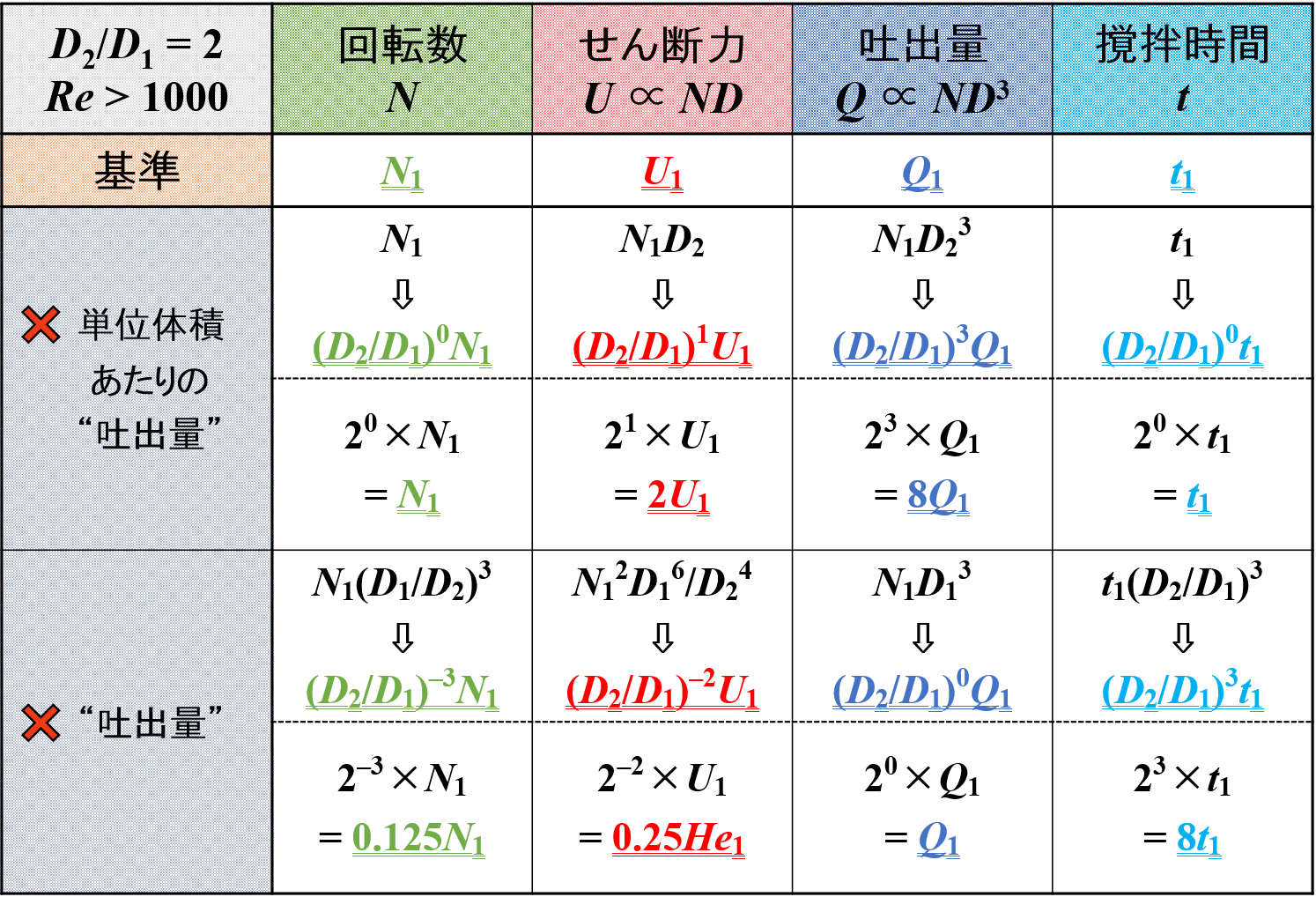
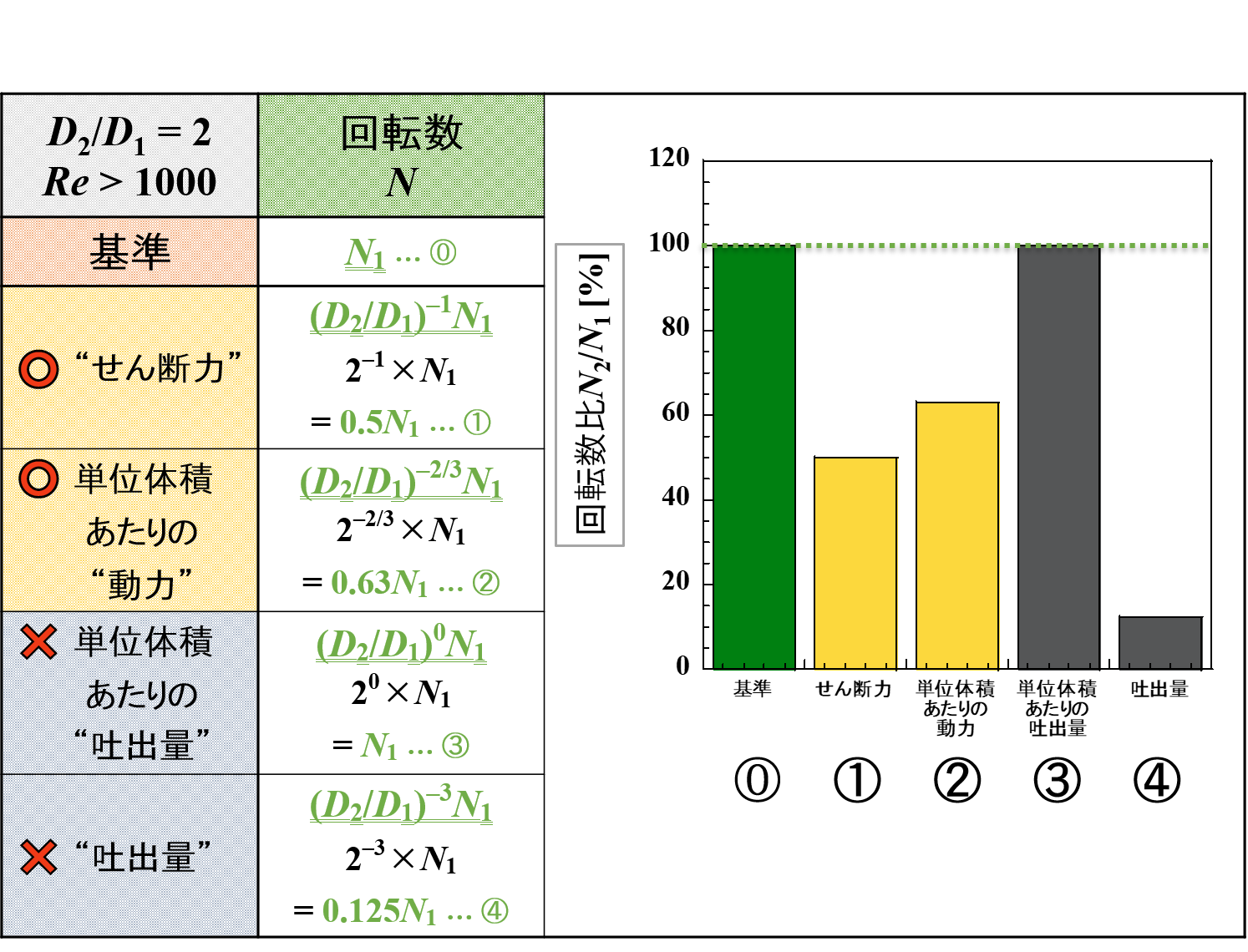
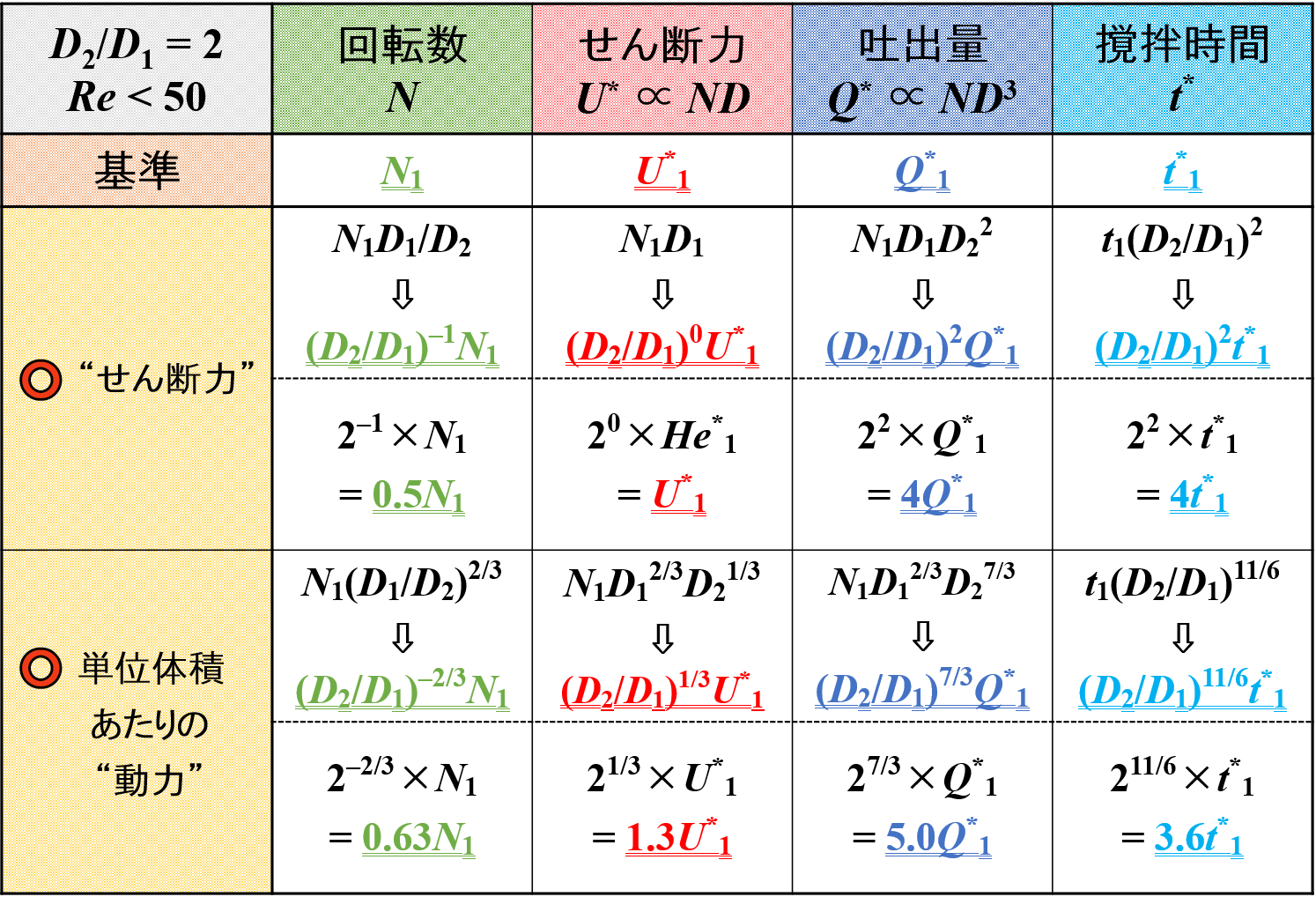
この中で，「回転数」と「撹拌時間」をピックアップして比較をしてみたいと思います。

スケールアップ後に羽根径が2倍になった（D₂/D₁ = 2）ときの変化量です。

各スケールアップ条件における特徴がイメージできるかと思います。

単位体積あたりの吐出量一定の条件では，回転数と撹拌時間が一定になっていることが改めてわかります。

---

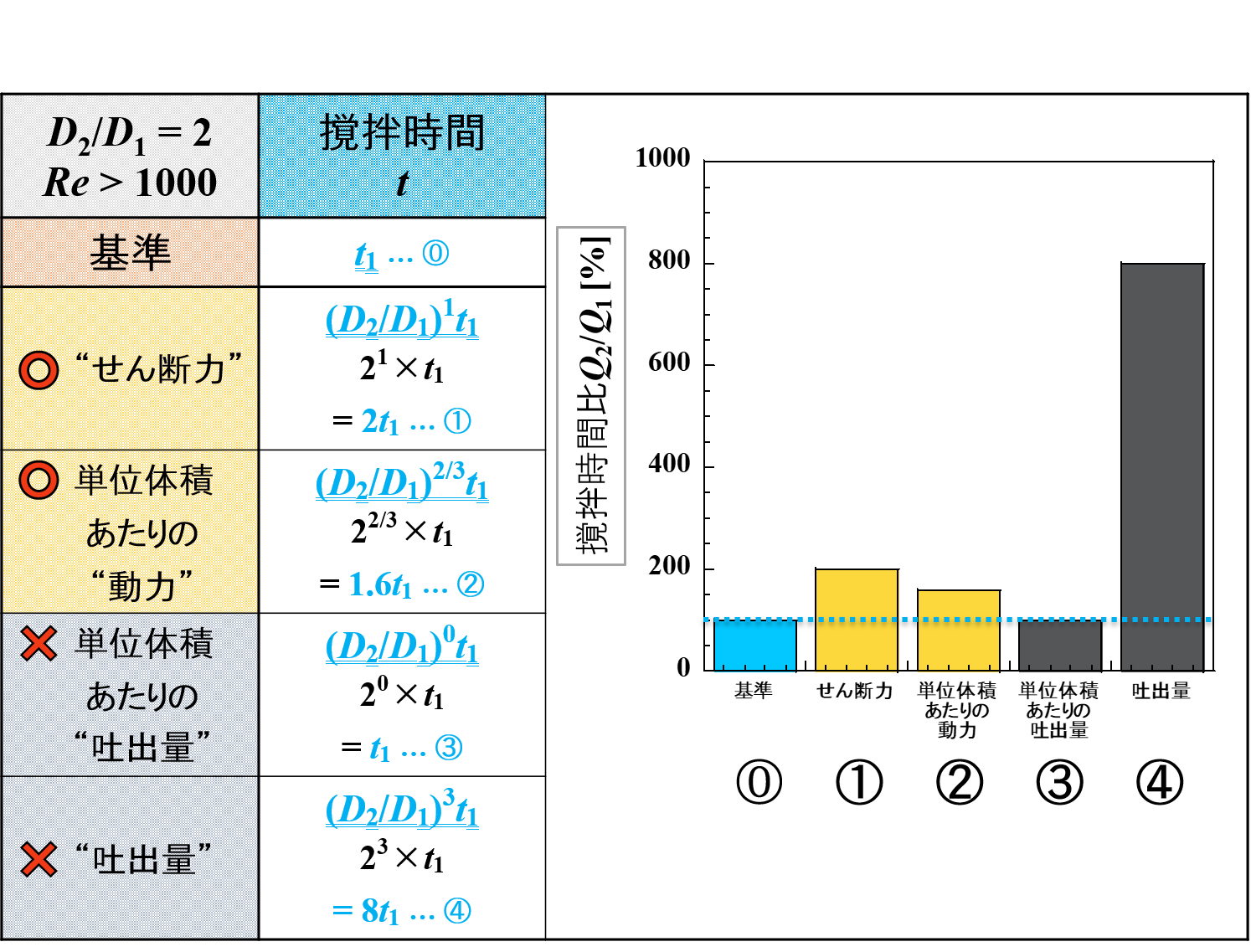
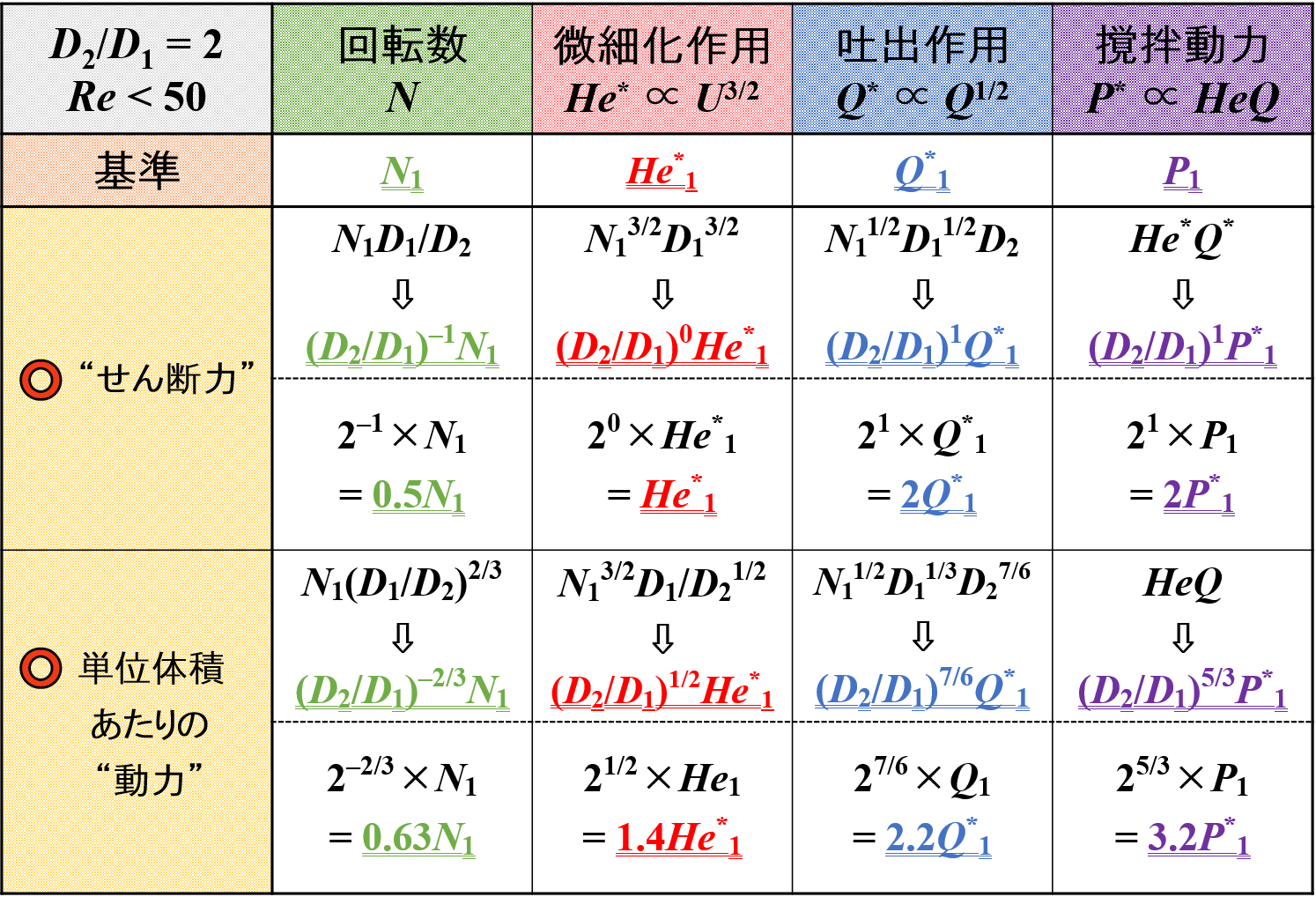
引き続き，下表に各種因子の変化を示しています。

せん断力は微細化作用に，吐出量は吐出作用に変換しています。

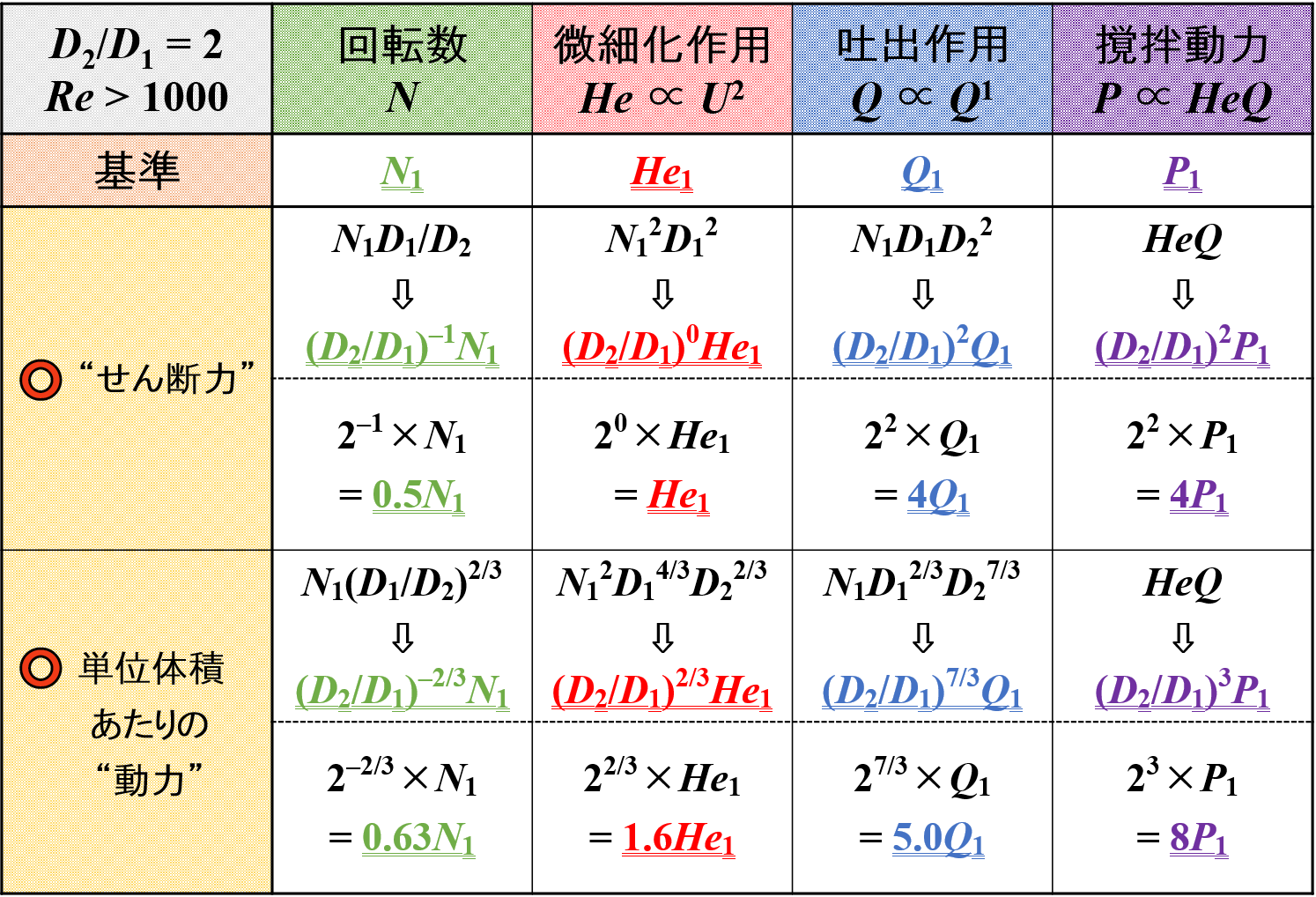
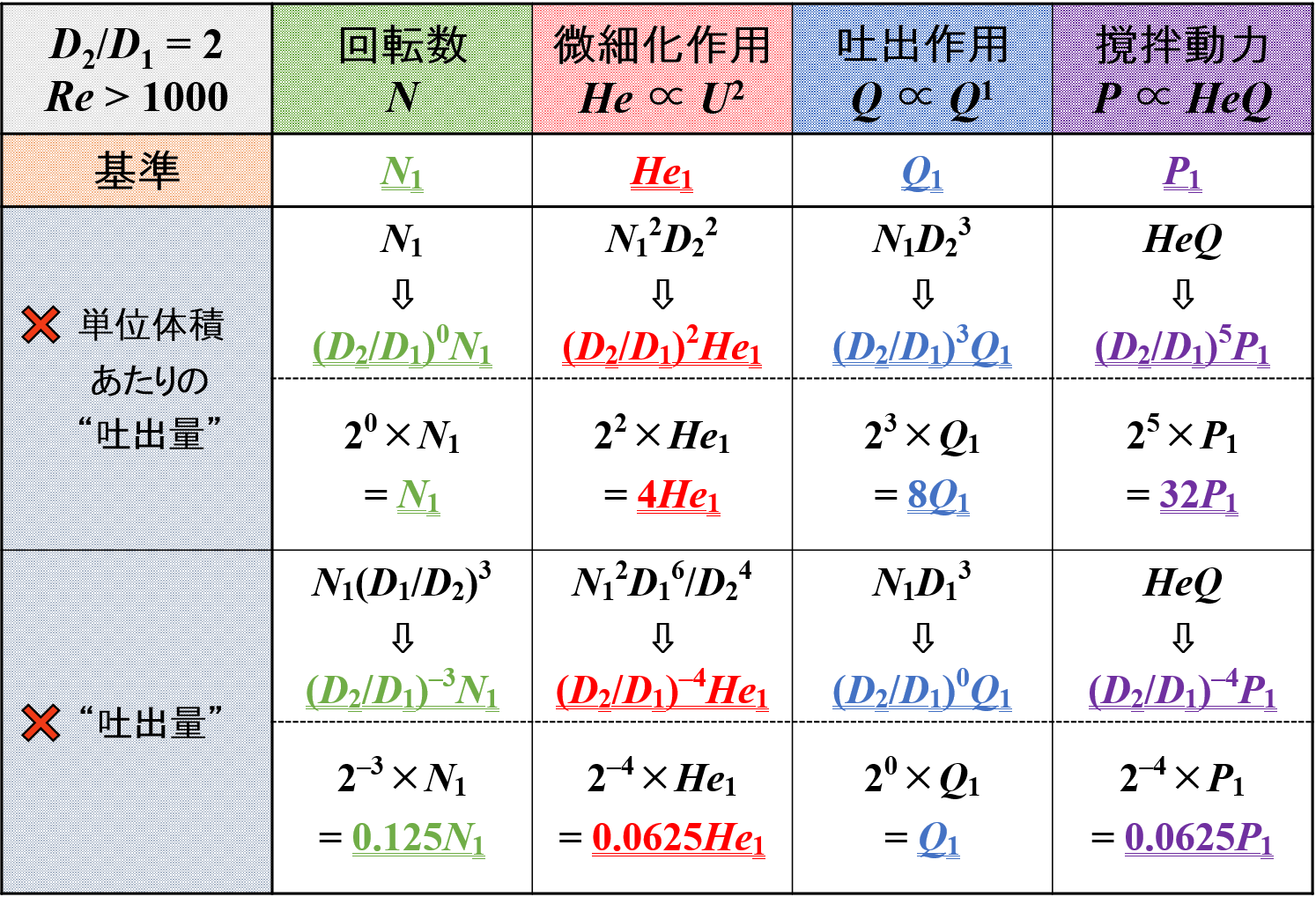
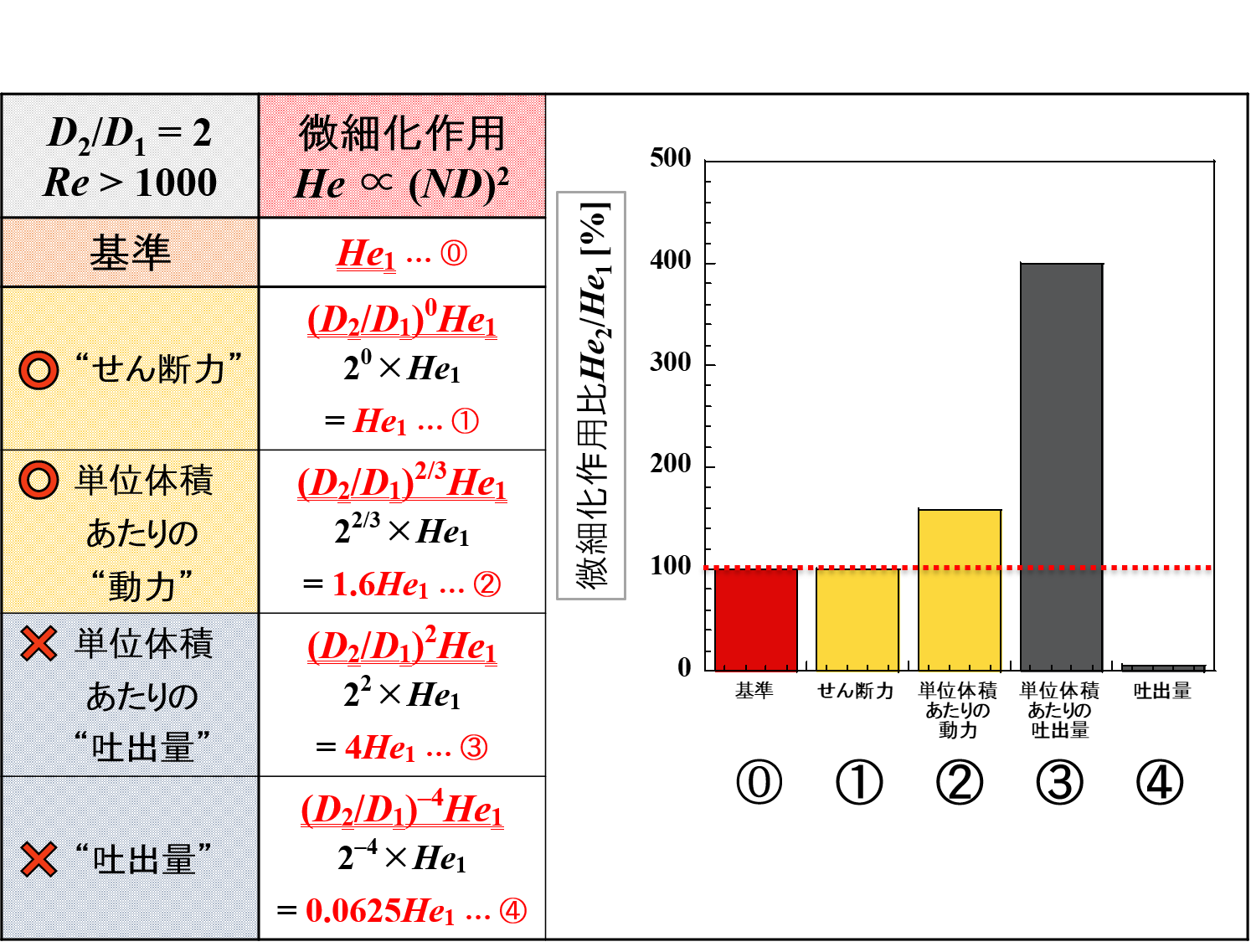
この中で，「微細化作用」と「吐出作用」をピックアップして比較をしてみたいと思います。

スケールアップ後に羽根径が2倍になった（D₂/D₁ = 2）ときの変化量です。

各スケールアップ条件における特徴がイメージできるかと思います。

せん断力一定の条件では微細化作用が，吐出量一定の条件では吐出作用が一定になっていることが改めてわかります。

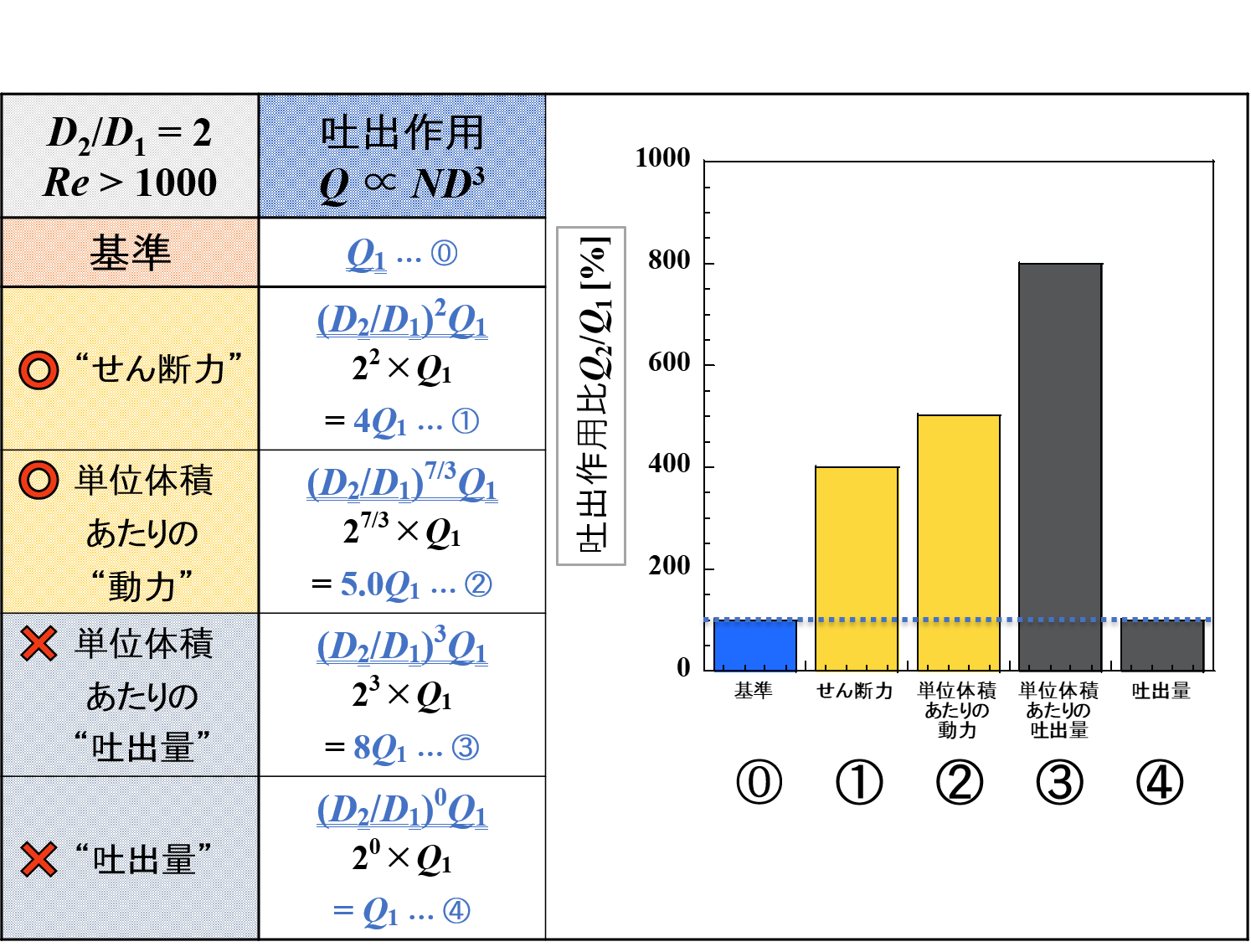
次に，撹拌動力（エネルギー）を考えます。

「撹拌をやさしく捉えてみよう【撹拌作用の使い分け】」のページで紹介したように，撹拌動力は微細化作用と吐出作用の積に比例します。

そこで，スケールアップ後に羽根径が2倍になった（D₂/D₁ = 2）と仮定して撹拌動力の変化を調べると，下表のようになります。

採用できない条件で極端な結果が出ていることがわかります。

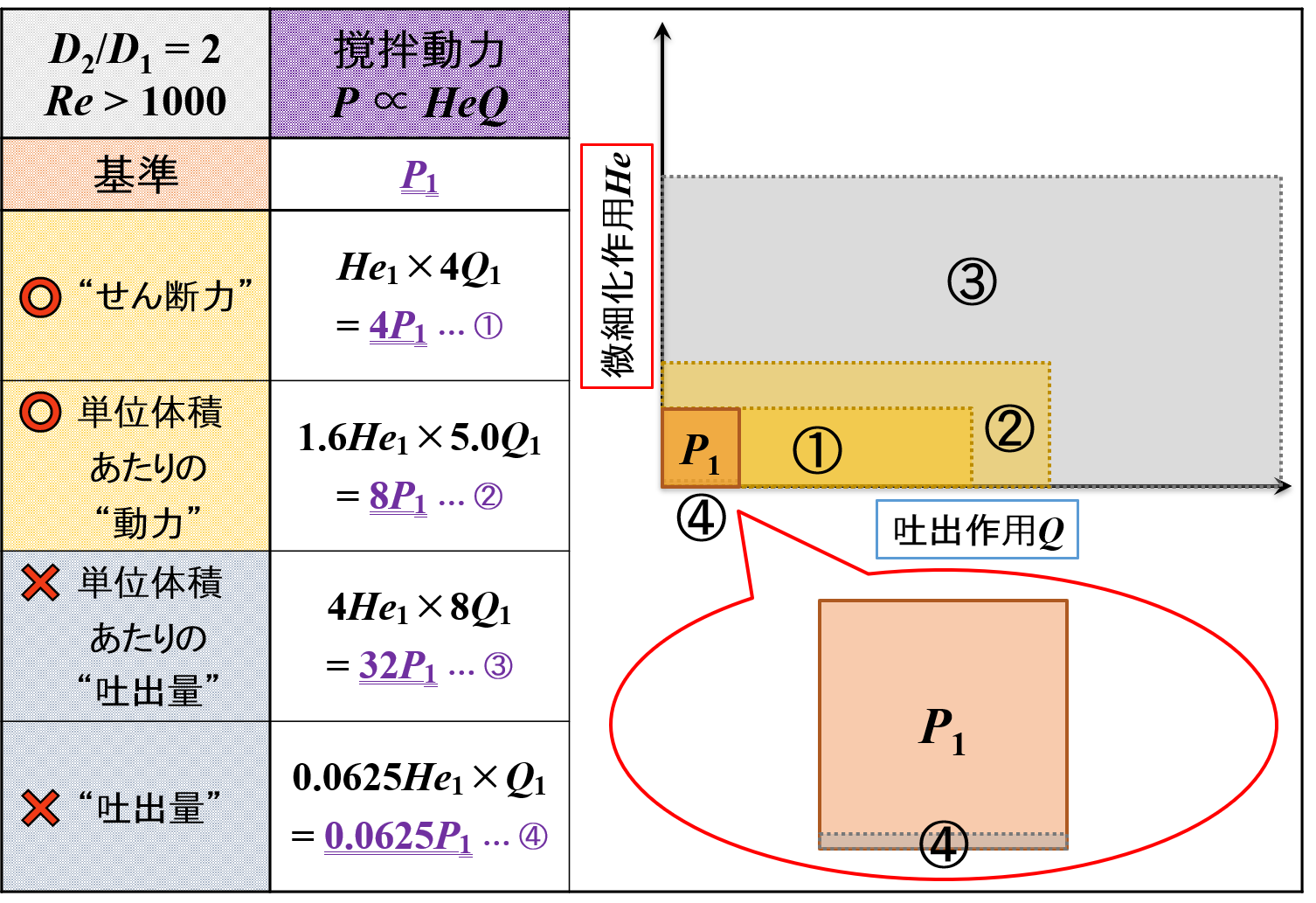
ここで，採用できない条件について注目したいと思います。

「スケールアップ理論を考えてみよう ー 乳化編【単位体積あたりの吐出量一定時における撹拌作用の変化】」のページで紹介したように，確かに非常に大きなモータを必要とすることがわかります。

📝[memo]　「スケールアップ理論を考えてみよう ー 乳化編【スケールアップによる製造規模の変更】」でも同じニュアンスの説明をしています。

一方，「スケールアップ理論を考えてみよう ー 乳化編【吐出量一定時における撹拌作用の変化】」のページで紹介した「吐出量一定」の条件は，小さなモータを使用することで済みそうです。

ただし，撹拌作用が小さいことを意味するので，非常に長い撹拌時間を必要とします。

📝[memo]　結果として，生産効率が非常に悪いと言えます。

このように考えると，採用できない条件がイメージしやすくなります。

層流域

採用できる「せん断力一定」と「単位体積あたりの動力一定」の条件に限っていますが，層流域における各種因子の変化も見てみましょう。

📝[memo]　上述したように，撹拌作用は撹拌レイノルズ数の影響を受けます。

計算過程は省略しますが，乱流域の場合と同じように考えると下表の結果が得られます。

スケールアップ後に羽根径が2倍になった（D₂/D₁ = 2）と仮定して各種因子の変化を考えることにします。

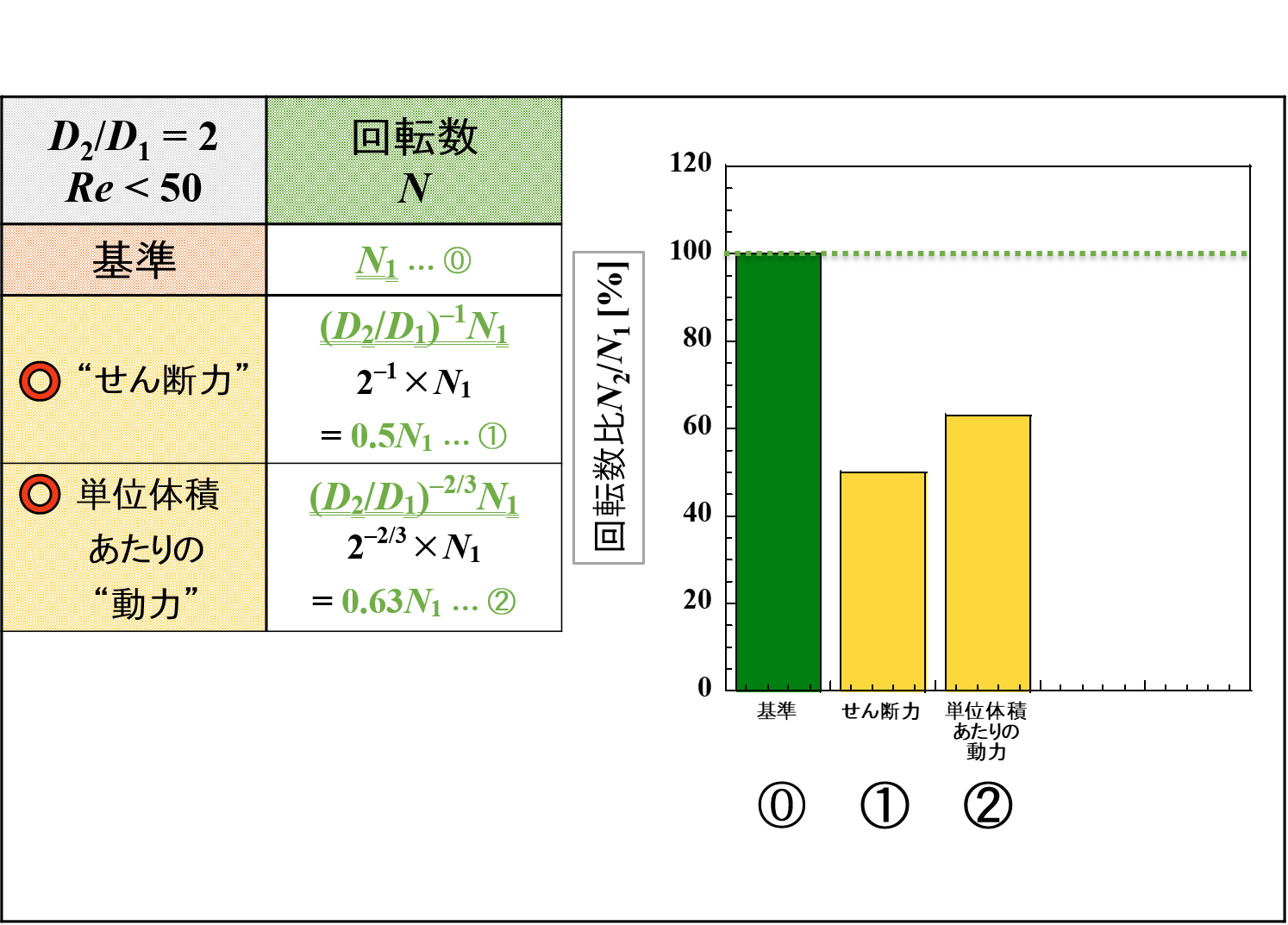
この中で，「回転数」と「撹拌時間」をピックアップして比較をしてみたいと思います。

スケールアップ後に羽根径が2倍になった（D₂/D₁ = 2）ときの変化量です。

ここでは，イメージだけの紹介となります。

---

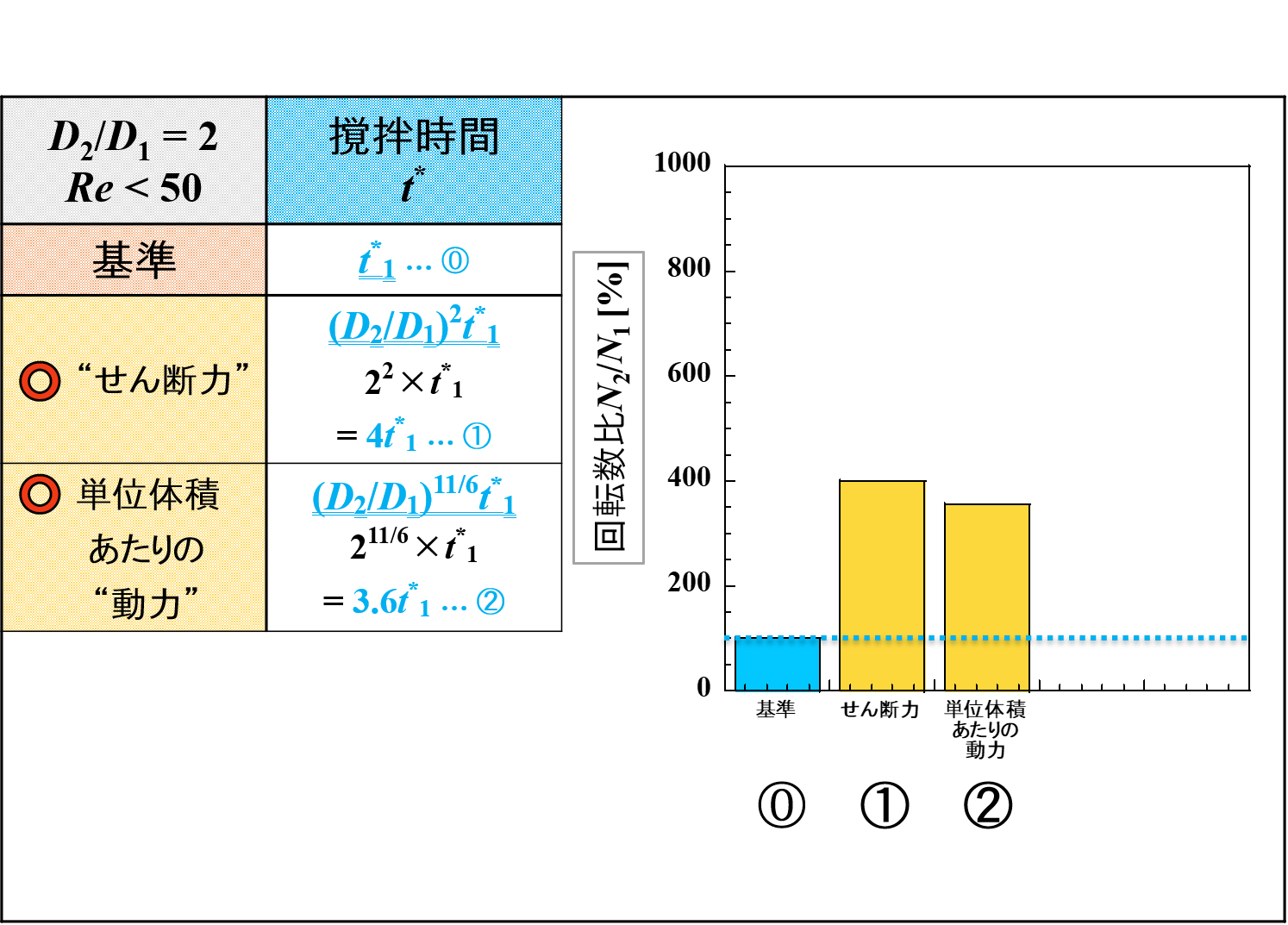
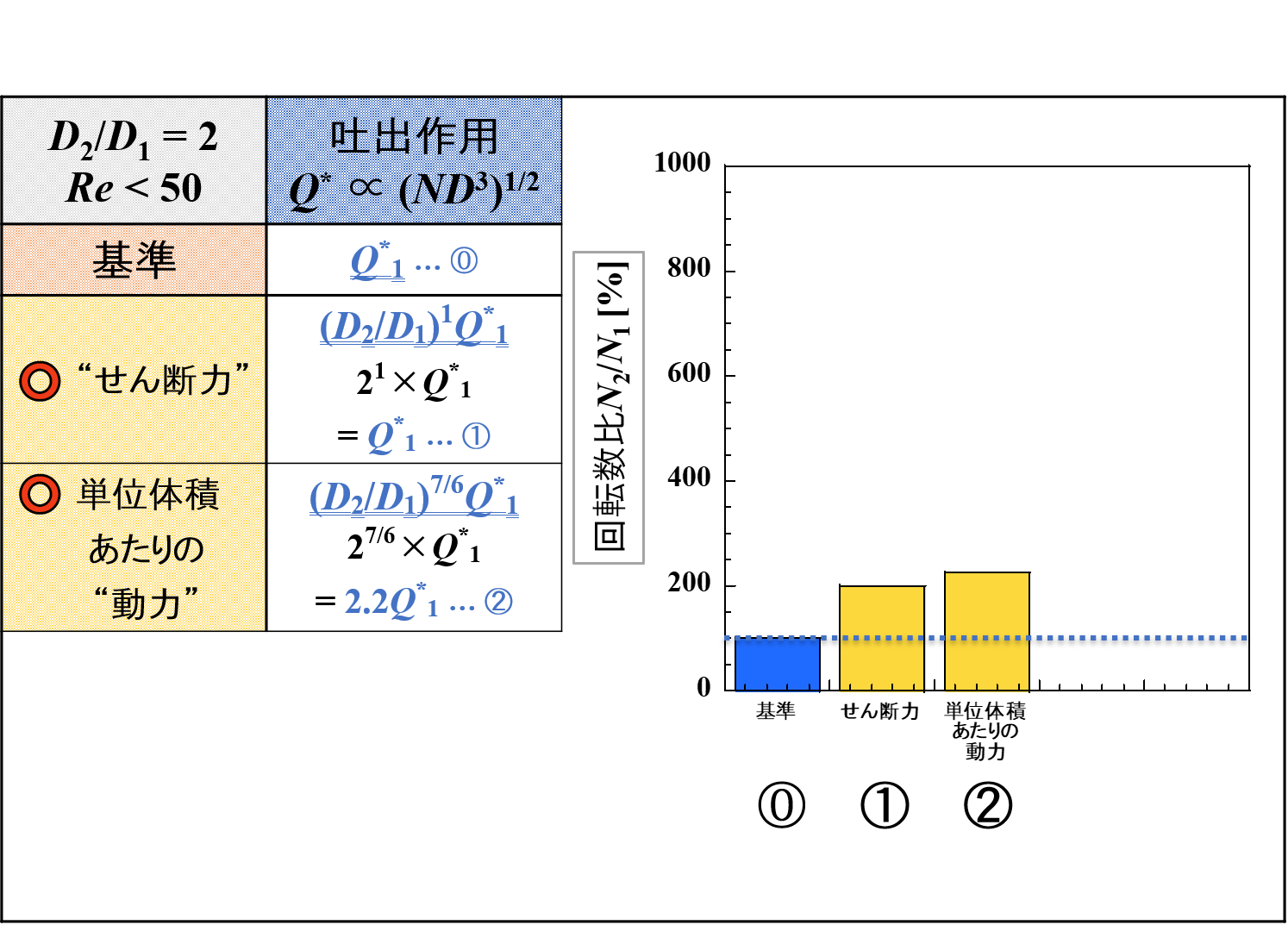
引き続き，下表に各種因子の変化を示しています。

せん断力は微細化作用に，吐出量は吐出作用に変換しています。

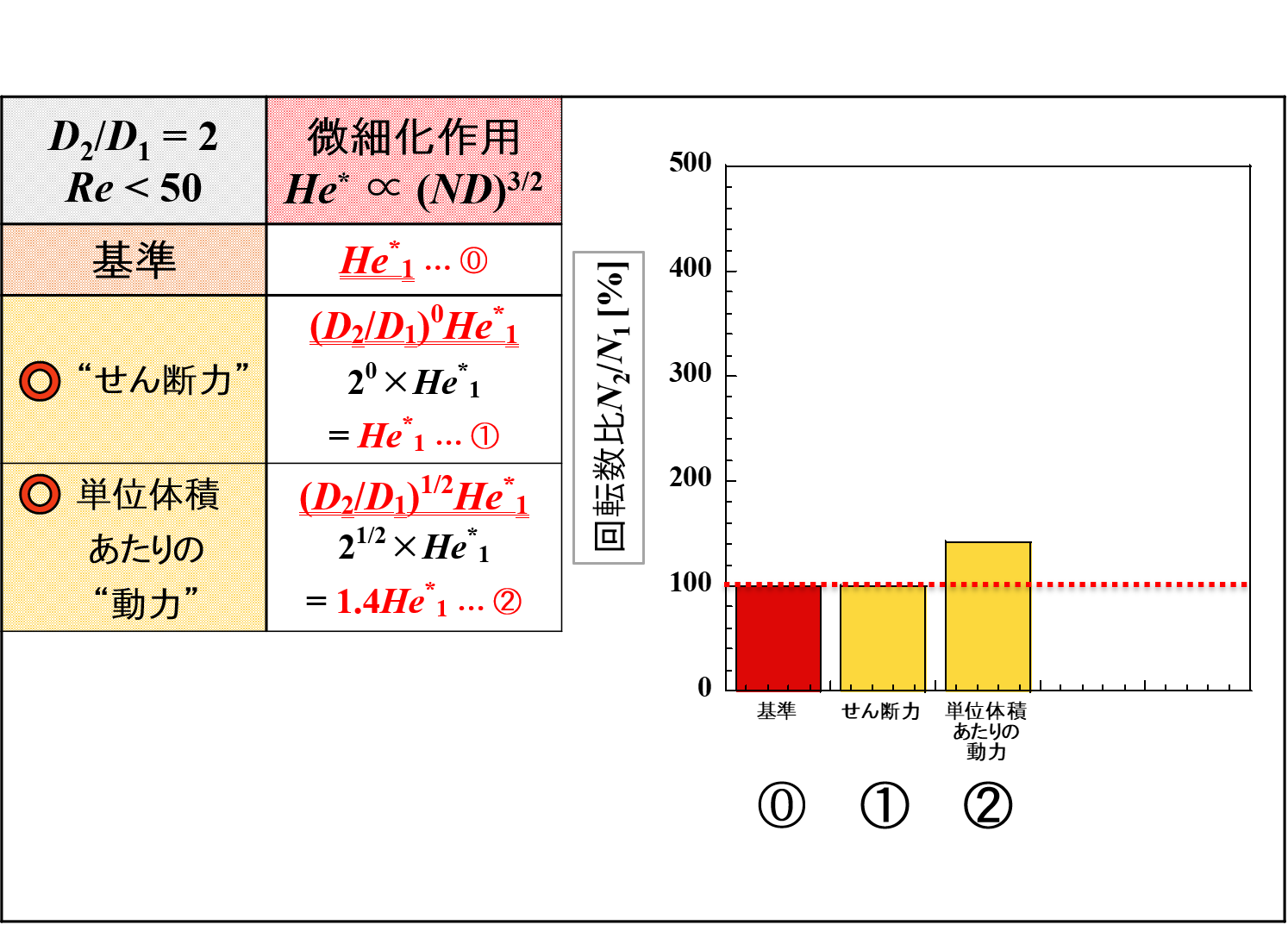
この中で，「微細化作用」と「吐出作用」をピックアップして比較をしてみたいと思います。

スケールアップ後に羽根径が2倍になった（D₂/D₁ = 2）ときの変化量です。

せん断力一定の条件では，撹拌レイノルズ数に関係なく微細化作用が一定になっていることが改めてわかります。

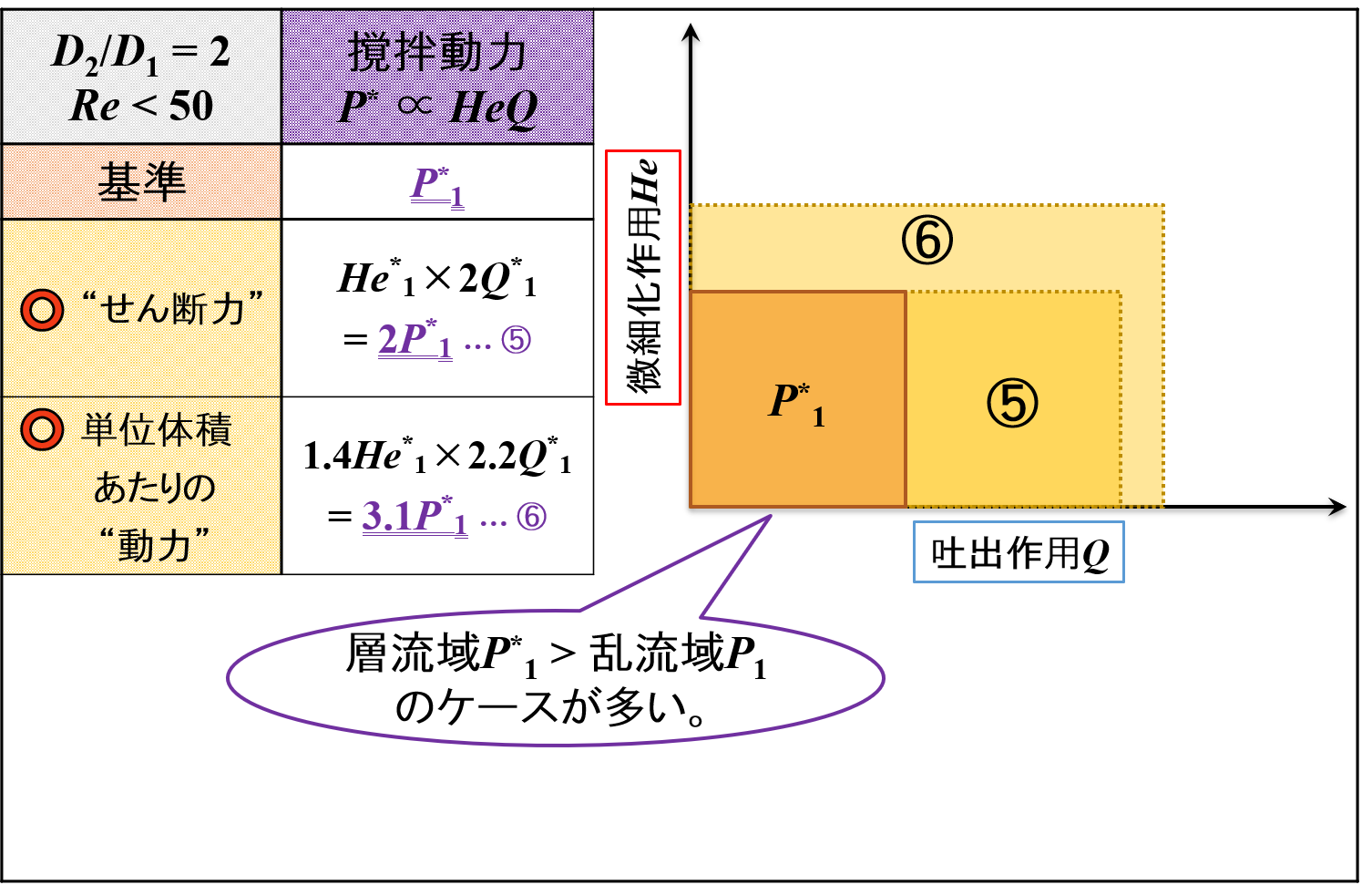
乱流域の場合と同様にして撹拌動力の変化を調べると，下表のようになります。

乱流域と層流域で変化の仕方に違いがあることがわかります。

このとき，「層流域P^*₁ = 乱流域P₁」ではない点に注意が必要です。

スケールアップ後を考えたとき，P^*₂ = 2P^*₁，P₂ = 4P₁であるので，乱流域の方が大きな動力を必要となるように見えてしまいます。

実際は，「層流域P^*₁ > 乱流域P₁」のケースが多いです。
これは，「スケールアップ理論を考えてみよう ー 乳化編【撹拌機が行う仕事】」のページで紹介した抵抗係数に着目すると，乱流域の方が大きな値になっていることからも理解できます。

📝[memo]　層流域は特殊な考えなので，この辺にしておきましょう。

スケールアップの計算結果とその実証

色々と複雑なことを考えてきましたが，ホモミキサーの話に戻してみましょう。

特にホモミキサーにおいては，”せん断力をを等しくすること”と”パス回数を等しくすること”で，せん断力を一定にする条件を採用しました。

一方で，様々なスケールアップ条件がありましたが，すべてを満たすことができないことがわかります。

すなわち，ホモミキサーによる乳化モデルは本質的に不確定な要素を含むことを意味します。

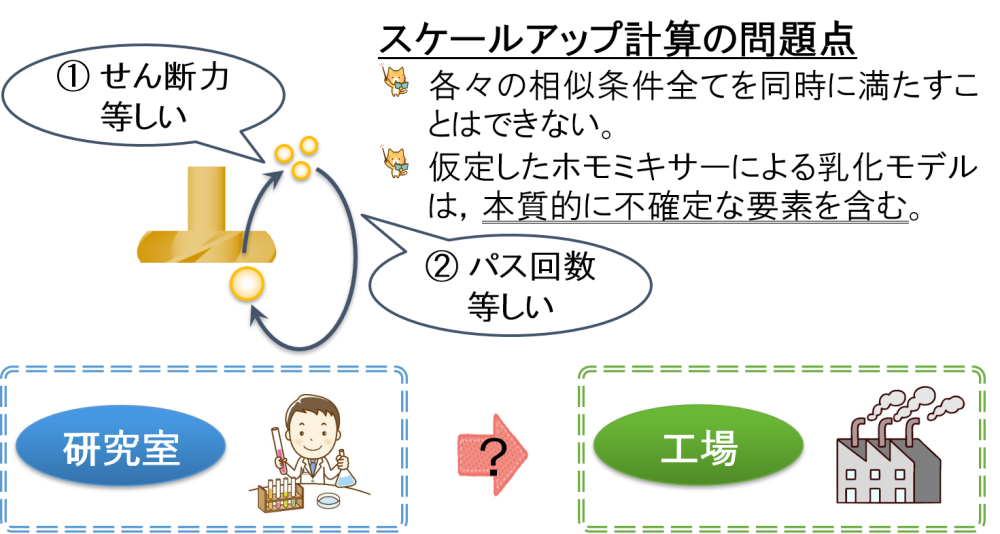
このようにしてホモミキサーを中心としたスケールアップ理論を考えることができますが，理想的な撹拌条件を設定できない事情があります。

すると，どこかで妥協せざるを得ないのですが，本当にスケールアップができているのかわからなくなります。

したがって，スケールアップ計算における結果の正否について，実際の試作を行い見極める必要があります。