一般的なパドル（プロペラ）ミキサーのスケールアップ

「スケールアップ理論を考えてみよう ー 乳化編【“N^3D^2”とは？】」で紹介した計算式を使って，具体的にスケールアップ後の条件を算出してみたいと思います。

スケールアップをするにあたって，下図における4000 L (4 m³)撹拌槽の条件が最適であったと仮定します。

そして，この条件を基に12000 L (12 m³)撹拌槽へスケールアップすることを考えます。

パドルミキサーによるスケールアップ計算で必要となる因子について確認しておきましょう。

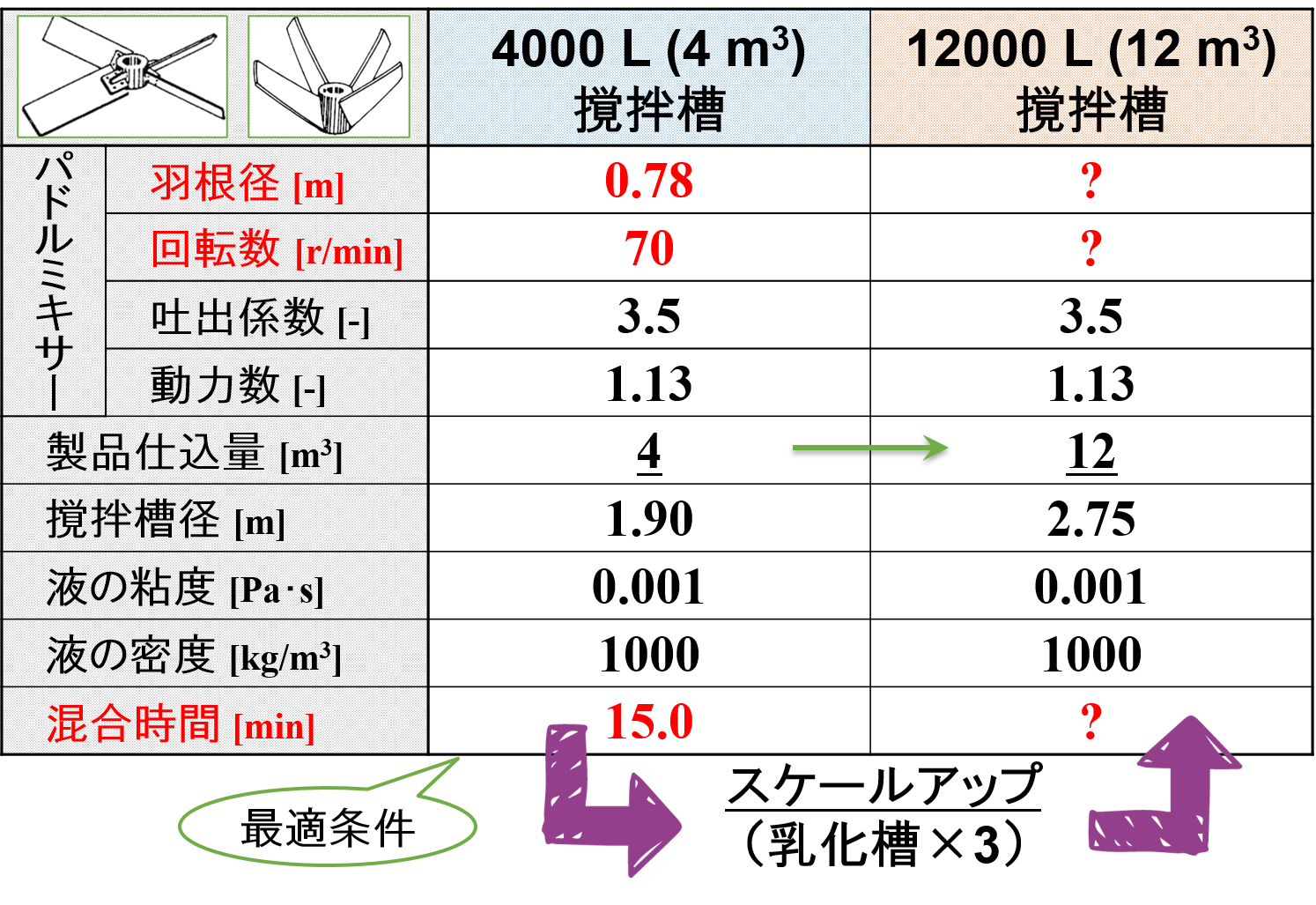
4000 L (4 m³)撹拌槽

• 羽根径 [m]　👉　4 m³撹拌槽で使用するパドルミキサーは決まっているので，自然に確定する値となります。
• 回転数 [r/min]　👉　4 m³撹拌槽にて決定した最適条件によって決まるので，実験によって確定する値となります。
• 吐出係数 [-]・動力数 [-]　👉　4 m³撹拌槽で使用するパドルミキサーは決まっているので，自然に確定する値となります。
• 製品仕込量 [m³]　👉　製品仕込量は任意なので，自分で確定する値となります。
• 撹拌槽径 [m]　👉　4 m³撹拌槽は決まっているので，自然に確定する値となります。
• 液の粘度 [Pa・s]　👉　4 m³撹拌槽で製造する製品は決まっているので，自然に確定する値となります。
• 密度 [kg/m³]　👉　4 m³撹拌槽で製造する製品は決まっているので，自然に確定する値となります。
• 混合時間 [min]　👉　4 m³撹拌槽にて決定した最適条件によって決まるので，実験によって確定する値となります。

12000 L (12 m³)撹拌槽

• 羽根径 [m]　👉　幾何学的相似を満たすようにして算出する値となります。（未知数）
• 回転数 [r/min]　👉　パドルミキサーによるスケールアップ計算で算出する値となります。（未知数）
• 吐出係数 [-]・動力数 [-]　👉　12 m³撹拌槽で使用するパドルミキサーは決まっているので，自然に確定する値となります。
• 製品仕込量 [m³]　👉　製品仕込量は任意なので，自分で確定する値となります。
• 撹拌槽径 [m]　👉　12 m³撹拌槽は決まっているので，自然に確定する値となります。
• 液の粘度 [Pa・s]　👉　12 m³撹拌槽で製造する製品は決まっているので，自然に確定する値となります。
• 密度 [kg/m³]　👉　12 m³撹拌槽で製造する製品は決まっているので，自然に確定する値となります。
• 混合時間 [min]　👉　パドルミキサーによるスケールアップ計算で算出する値となります。（未知数）

12 m³撹拌槽における羽根径・回転数・混合時間は，算出する値（未知数）です。

そこで，これら羽根径・回転数・乳化時間を算出することにします。

パドルミキサーの計算例⑴（4 m³ → 12 m³仕込み・パドルミキサーの直径）

以降，○₄（添え字＝4）は4 m³撹拌槽，○₁₂（添え字＝12）は12 m³撹拌槽のときの値を示します。

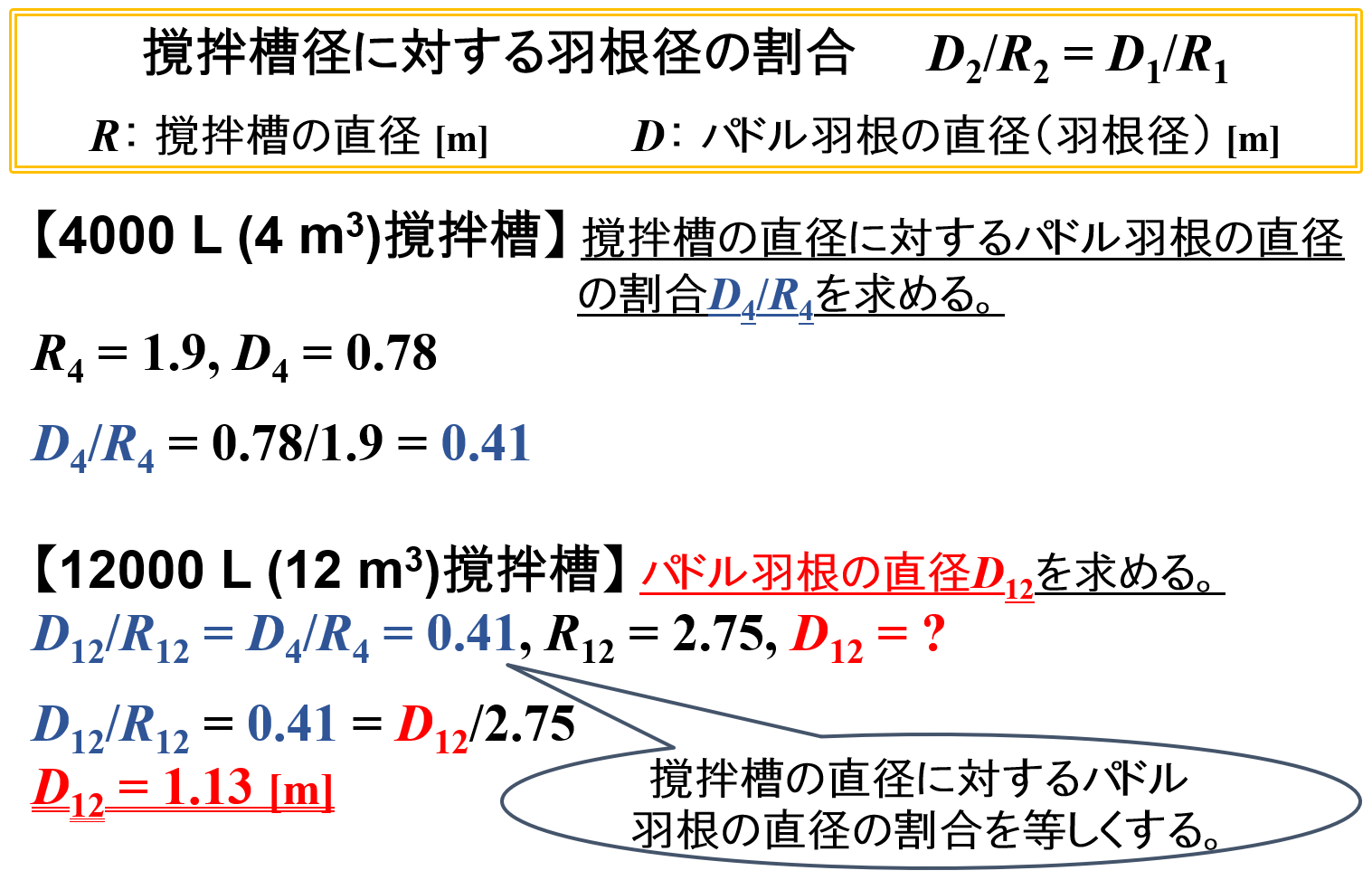
撹拌槽径R₄，羽根径D₄は既知であるので，撹拌槽径に対する羽根径の割合D₄/R₄をを求めます。

D4/R₄ = 0.78/1.9 = 0.41

次に，4 m³撹拌槽と12 m³撹拌槽との間で幾何学的相似を満たすとき，D₁₂/R₁₂ = D₄/R₄ = 0.41が成り立ちます。

そして，既知である撹拌槽径R₄，羽根径D₄をこの式に代入して，羽根径D₁₂を求めます。

D₁₂/R₁₂ = 0.41 = D₁₂/2.75

D₁₂ = 1.13 [m]

以上より，12 m³撹拌槽におけるパドルミキサーの羽根径D₁₂を算出することができました。

パドルミキサーの計算例⑵（4 m³ → 12 m³仕込み・単位体積あたりの動力～回転数）

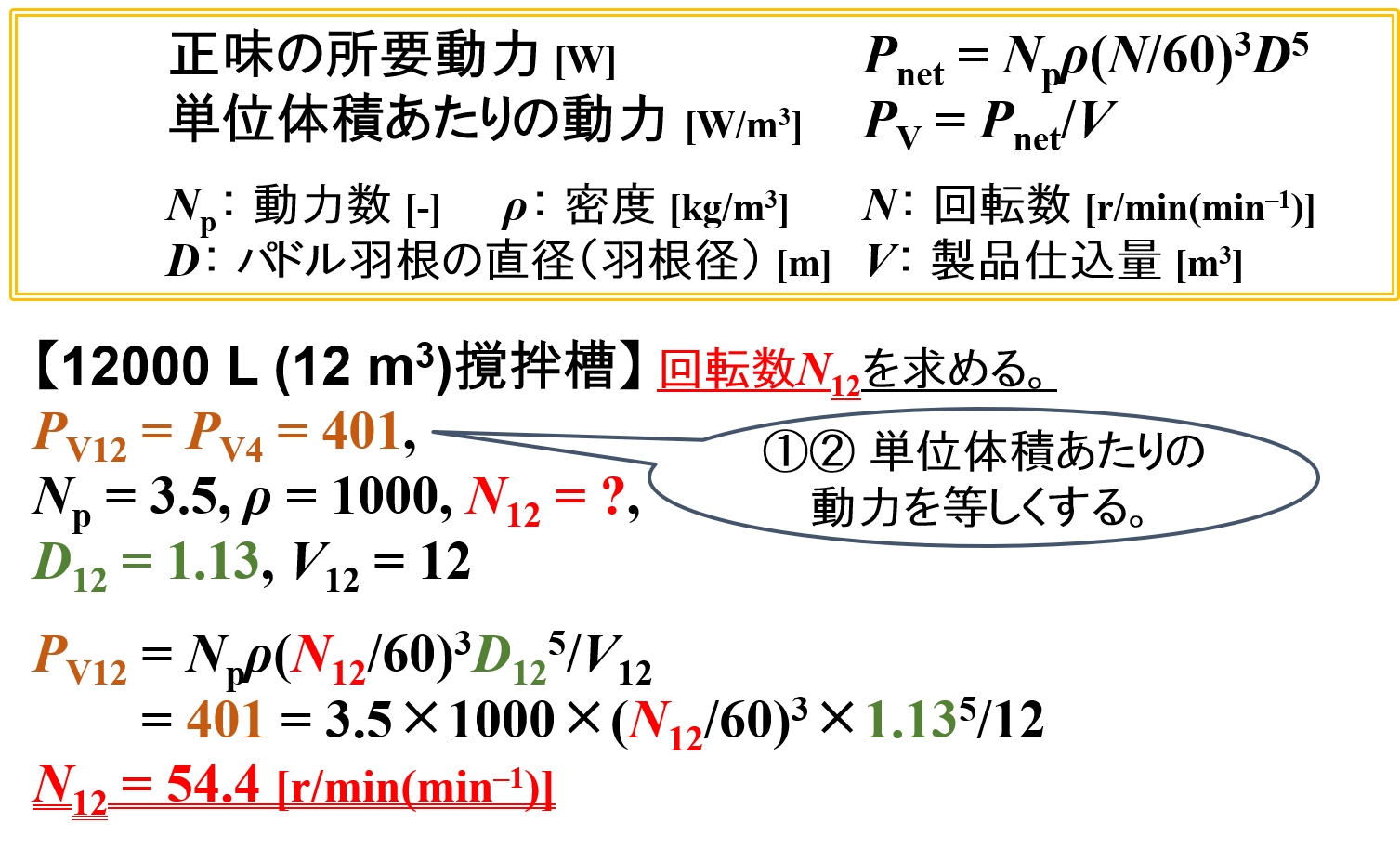
最適な回転数N₄，羽根径D₄，動力数N_p，製品の密度ρ，製品仕込量V₄が既知であるので，これらを単位体積あたりの動力の式に代入して単位体積あたりの動力P_V4をを求めます。

P_V4 = N_pρ(N₄/60)³D₄⁵/V₄ = 3.5×1000×(70/60)³×0.78⁵/4 = 401 [W/m³]

一方，「”（条件①）平均液滴径が等しくなるようにする”という考え方」＝「”（条件②）物質移動速度が等しくなるようにする”という考え方」＝「”単位体積あたりの動力を等しくする”という考え方」であるので，12 m³撹拌槽における単位体積あたりの動力P_V12も401 [W/m³]となります。

さらに，既知である単位体積あたりの動力P_V12，羽根径D₁₂，動力数N_p，製品の密度ρ，製品仕込量V₁₂を単位体積あたりの動力の式に代入して，最適な回転数N₁₂を求めます。

P_V12 = N_pρ(N₁₂/60)³D₁₂⁵/V₁₂ = 401 = 3.5×1000×(N₁₂/60)³×1.13⁵/12

N₁₂ = 54.4 [r/min(min^–1)]

以上より，12 m³撹拌槽におけるパドルミキサーの回転数N₁₂を算出することができました。

パドルミキサーの計算例⑶（4 m³ → 12 m³仕込み・吐出量）

続いて，吐出係数N_q4も既知であるので，これと最適な回転数N₄，羽根径D₄を吐出量の式に代入して，吐出量Q₄を求めます。

📝[memo]　やっていることは，「スケールアップ理論を考えてみようー乳化編【ホモミキサーのスケールアップ検討例①】」で紹介した内容と同じです。

このとき，「スケールアップ理論を考えてみよう ー 乳化編【“ホモミキサー”による吐出量】」のページで紹介したように，実際の製品であっても（水の）吐出係数N_qを使用します。

Q₄ = N_q4N₄D₄³・10³ = 1.13×70×0.78³×1000 = 3.75×10⁴ [L/min]

📝[memo]　パドルミキサーは吐出作用が得意なので，ホモミキサーと比べて吐出係数N_qが大きいことがわかります。（0.1 → 1.13）

同様にして，既知である吐出係数N_q12，羽根径D₁₂，そして算出した回転数N₁₂を吐出量の式に代入して，吐出量Q₁₂を求めます。

Q₁₂ = N_q12N₁₂D₁₂³・10³ = 1.13×54.4×1.13³×1000 = 8.87×10⁴ [L/min]

以上より，4 m³撹拌槽および12 m³撹拌槽におけるパドルミキサーの吐出量Q₄とQ₁₂を算出することができました。

パドルミキサーの計算例⑷-1（4 m³ → 12 m³仕込み・循環回数～混合時間）

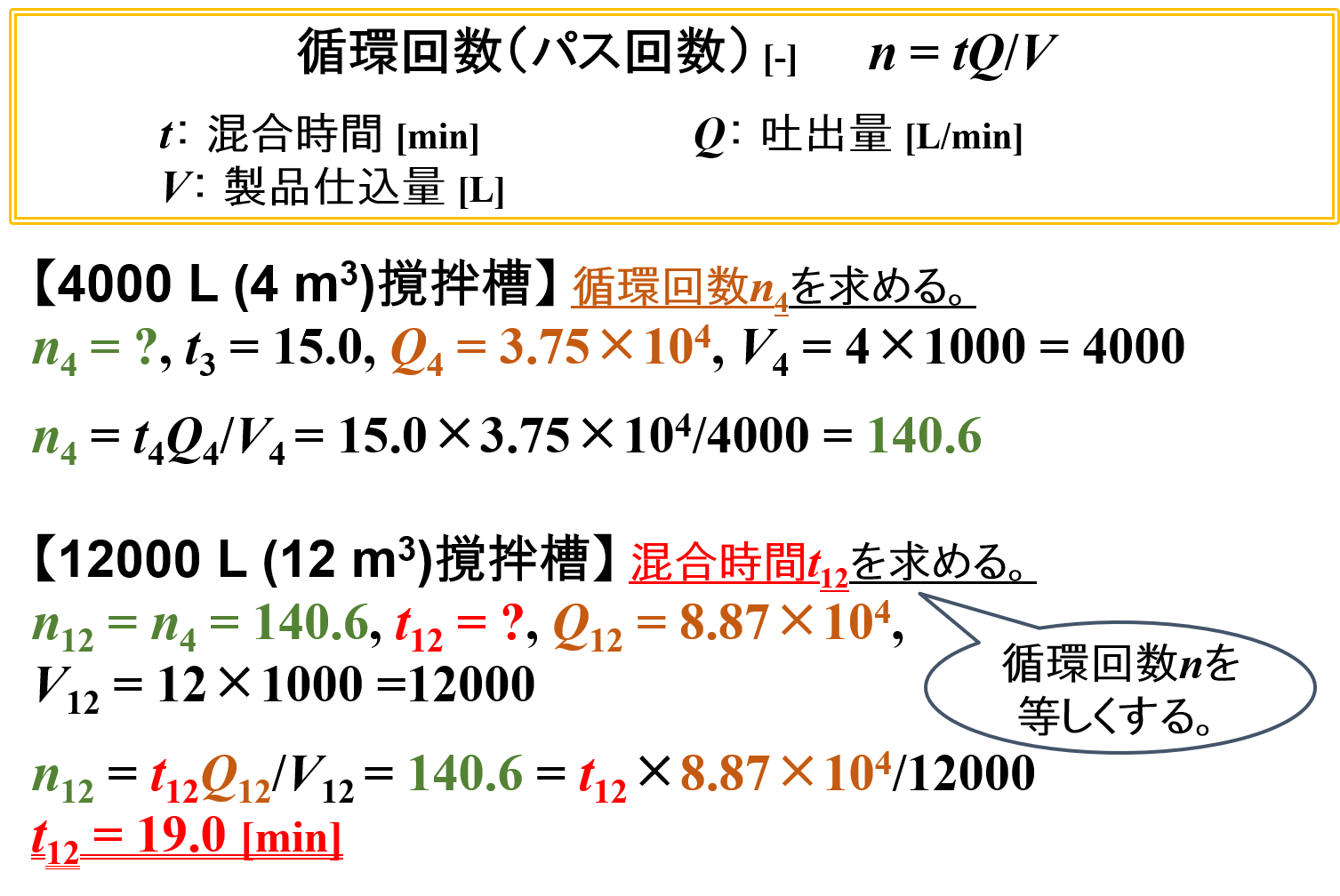
最後に，既知である最適な混合時間t₄，製品仕込量V₄，そして算出した吐出量Q₄を循環回数（パス回数）の式に代入して，循環回数n₄を求めます。

📝[memo]　やっていることは，「スケールアップ理論を考えてみようー乳化編【ホモミキサーのスケールアップ検討例①】」で紹介した内容と同じです。

📝[memo]　最初に，ホモミキサーと同様に循環回数（パス回数）が等しくなれば良い！という考え方で混合時間を算出しています。

n₄ = t₄Q₄/V₄ = 15.0×3.75×10⁴/4000 = 140.6

次に，12 m³撹拌槽と4 m³撹拌槽の循環回数nが等しいとするので，n₁₂ = n₄となる関係式が得られます。

さらに，既知である最適な混合時間t₁₂，製品仕込量V₁₂，そして算出した吐出量Q₁₂を循環回数の式に代入して，混合時間t₁₂をを求めます。

n₁₂ = t₁₂Q₁₂/V₁₂ = 140.6 = t₁₂×8.87×10⁴/12000

t₁₂ = 19.0 [min]

以上より，12 m³撹拌槽におけるパドルミキサーの混合時間t₁₂を算出することができました。

パドルミキサーの計算例⑸（4 m³ → 12 m³仕込み・撹拌レイノルズ数）

上述したように，ホモミキサーと同様に循環回数（パス回数）が等しくなれば良い！という考え方で混合時間を算出しましたが，無次元混合時間という考え方もありました。

📝[memo]　「スケールアップ理論を考えてみよう ー 乳化編【回転数・混合時間/乳化時間の考え方】」のページで，無次元混合時間について紹介しています。

また，無次元混合時間が適用できるためには，乱流域であることが求められます。

📝[memo]　「撹拌をやさしく捉えてみよう【撹拌による槽内の流動】」のページで，乱流域について紹介しています。

そこで，無次元混合時間を考える前に，4 m³撹拌槽と12 m³撹拌槽の撹拌レイノルズ数を計算しておきたいと思います。

最適な回転数N₄，羽根径D₄，製品の密度ρ，製品の密度ηが既知であるので，これらを撹拌レイノルズ数の式に代入して撹拌レイノルズ数Re₄をを求めます。

Re₄ = N₄D₄²ρ/60η = 70×0.78²×1000/(60×0.001) = 7.10×10⁵ > 1000 👉 乱流

その結果，乱流域であることが確認できました。

同様にして，最適な回転数N₁₂，羽根径D₁₂，製品の密度ρ，製品の密度ηが既知であるので，これらを撹拌レイノルズ数の式に代入して撹拌レイノルズ数Re₁₂を求めます。

Re₁₂ = N₁₂D₁₂²ρ/60η = 54.4×1.13²×1000/(60×0.001) = 1.16×10⁶ > 1000 👉 乱流

その結果，乱流域であることが確認できました。

スケールアップ前後で乱流域であることが確認できたので，続いて無次元混合時間を考えることにします。

📝[memo]　乱流域において，無次元混合時間は一定となりましたよね。

パドルミキサーの計算例⑹（4 m³ → 12 m³仕込み・無次元混合時間～混合時間）

最適な回転数N₄，混合時間t_M3が既知であるので，無次元混合時間t_M4N₄を求めます。

📝[memo]　表記が異なるだけで，「混合時間t＝混合時間t_M」を意味しています。

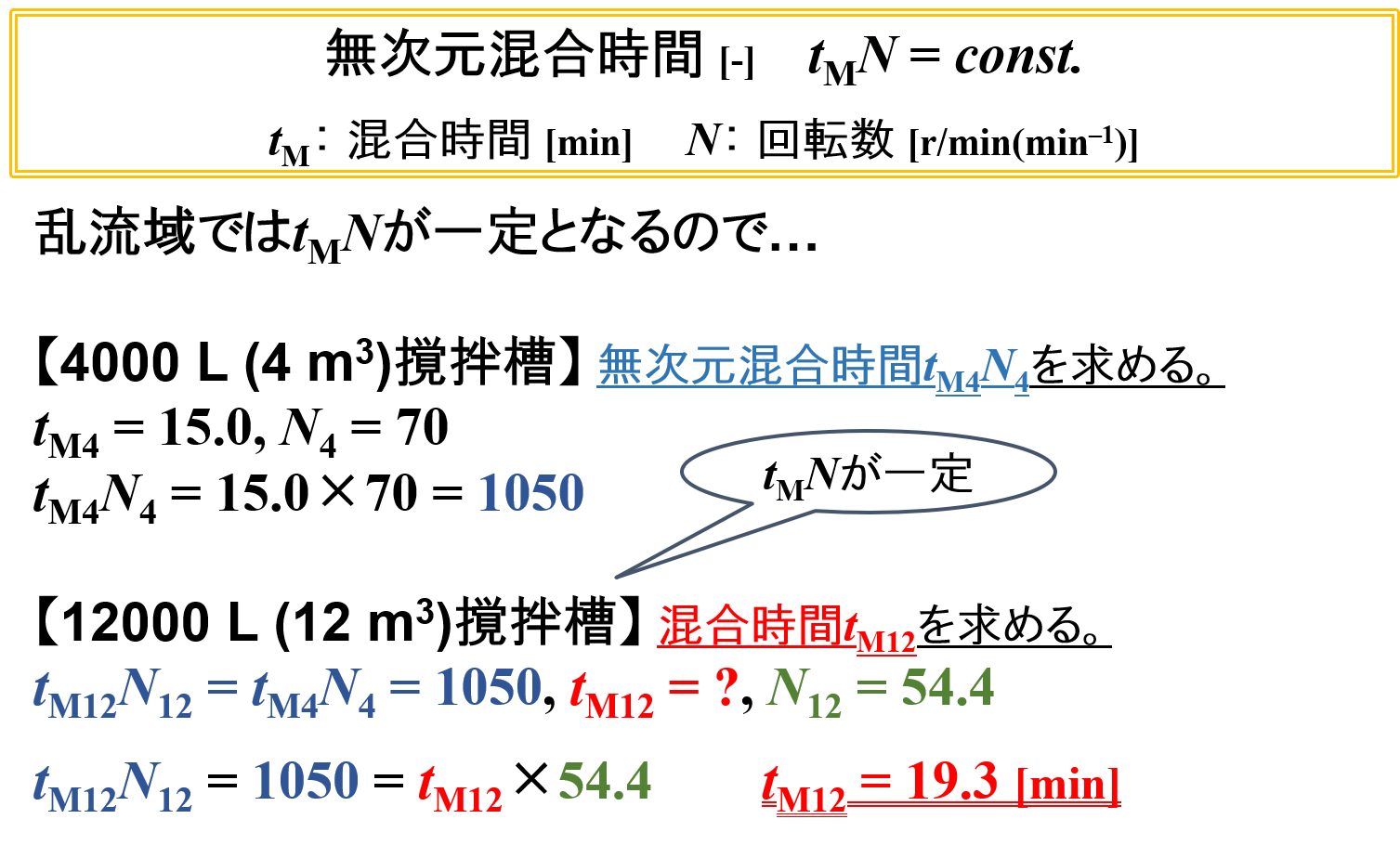
t_M4N₄ = 15.0×70 = 1050

一方，”無次元混合時間が等しくなるようにする”という考え方から，12 m³撹拌槽における無次元混合時間t_M12N₁₂も1050となります。

さらに，最適な回転数N₁₂が既知であるので，無次元混合時間の式に代入して混合時間t_M12を求めます。

t_M12N₁₂ = 1050 = t_M12×54.4

t_M12 = 19.3 [min]

以上より，12 m³撹拌槽におけるパドルミキサーの混合時間t_M12を算出することができました。

一般的なパドル（プロペラ）ミキサーのスケールアップ計算の結果

12 m³におけるパドルミキサーの羽根径・回転数・混合時間を算出することができました。

まとめると下図のようになります。

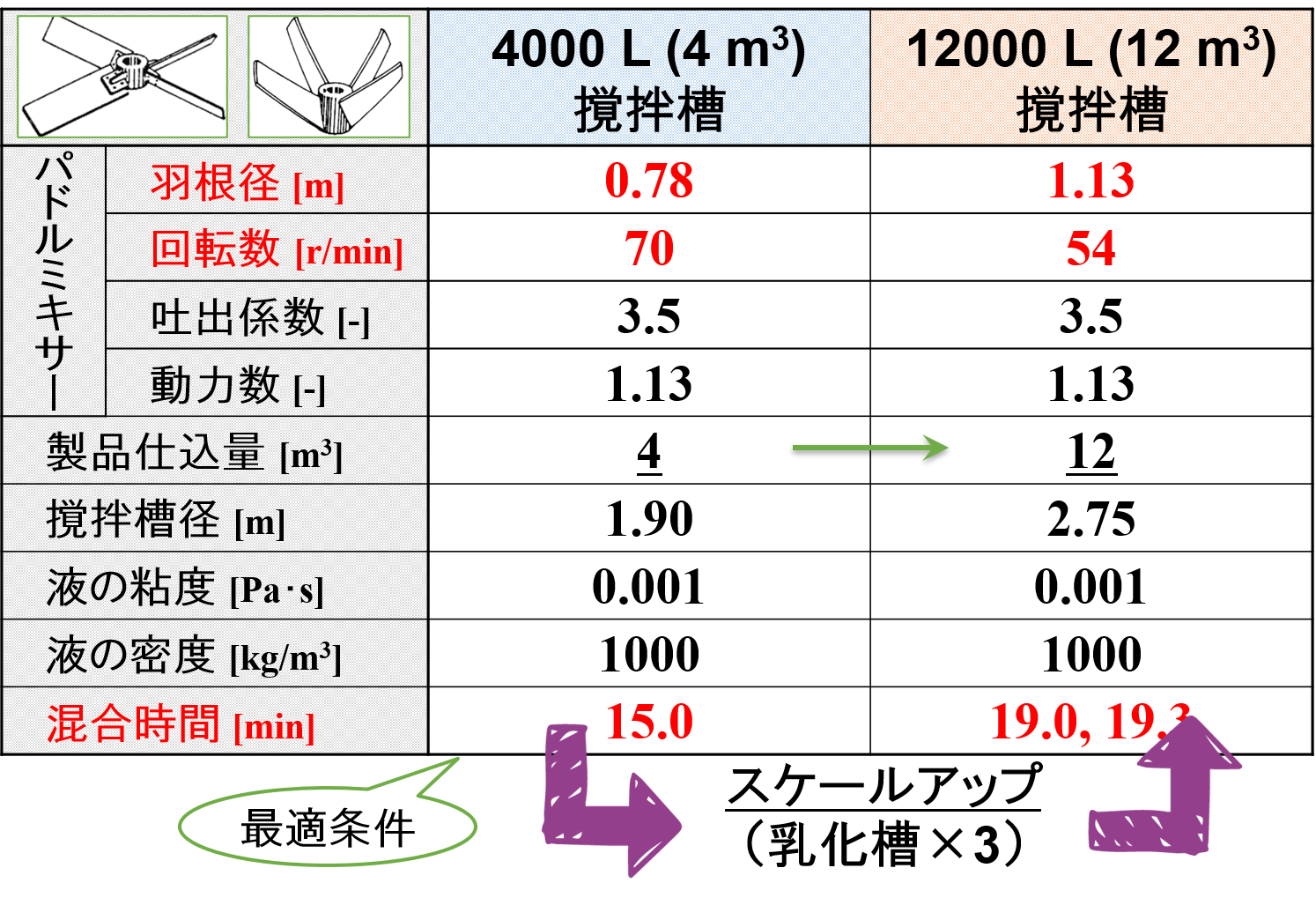
パドルミキサーの羽根径は，スケールアップ前後で幾何学的相似が満たされるように決定しました。

一方で，パドルミキサーによるスケールアップ計算で算出した回転数・混合時間は，「”単位体積あたりの動力を等しくする”という考え方」を採用して得られたものです。

「スケールアップ理論を考えてみよう ー 乳化編【単位体積あたりの動力一定時における撹拌作用の変化】」のページで紹介したように，スケールアップ前後で撹拌作用を一定にすることはできませんでした。

そのため，この条件で試作可能か否かの確認は必要となります。