単位体積あたりの吐出量

「スケールアップ理論を考えてみよう ー 乳化編【単位体積あたりの動力一定時における撹拌作用の変化】」のページで”単位体積あたりの吐出量”について触れました。

ここでは，それが意味するものについて考えます。

1秒あたりの吐出量

「スケールアップ理論を考えてみよう ー 乳化編【“ホモミキサー”による吐出量】」のページで紹介したように，吐出量の式は下式の通りでした。

「スケールアップ理論を考えてみよう ー 乳化編【“N^3D^2”とは？】」のページで紹介した正味の所要動力P_netと同じように，時間を[min] → [s]，体積を[L] → [m³]へ単位換算しておきましょう。

Q = N_qND³・10³　👉　Q = N_q(N/60)D³

単位体積あたりの吐出量Q_Vを決める因子

単位体積あたりの吐出量Q_Vがどのような式の形で表現できるか？を確認してみましょう。

Q_V = Q/V = N_q(N/60)D³/V

幾何学的相似により，V = αD³で表すことができるとします。

📝[memo]　体積は長さの3乗に比例するので，製品仕込量Vは羽根径Dの3乗に比例するとして，比例定数αを用いて表現しています。

Q_V = N_q(N/60)D³/αD³ = (N_q/α)(N/60) = (N_q/60α)N ∝ N

ここで，N_q/60αはスケールアップ前後で変化しません。

すなわち，単位体積あたりの吐出量Q_Vが”N”に比例することがわかります。

“単位体積あたりの吐出量一定”の一般式としての表し方

一般的に，「N₂/N₁ = 1」と表されることがあります。

下図に記載されているような計算をすることによって，最終的にこのような結論が得られます。

スケールアップ前

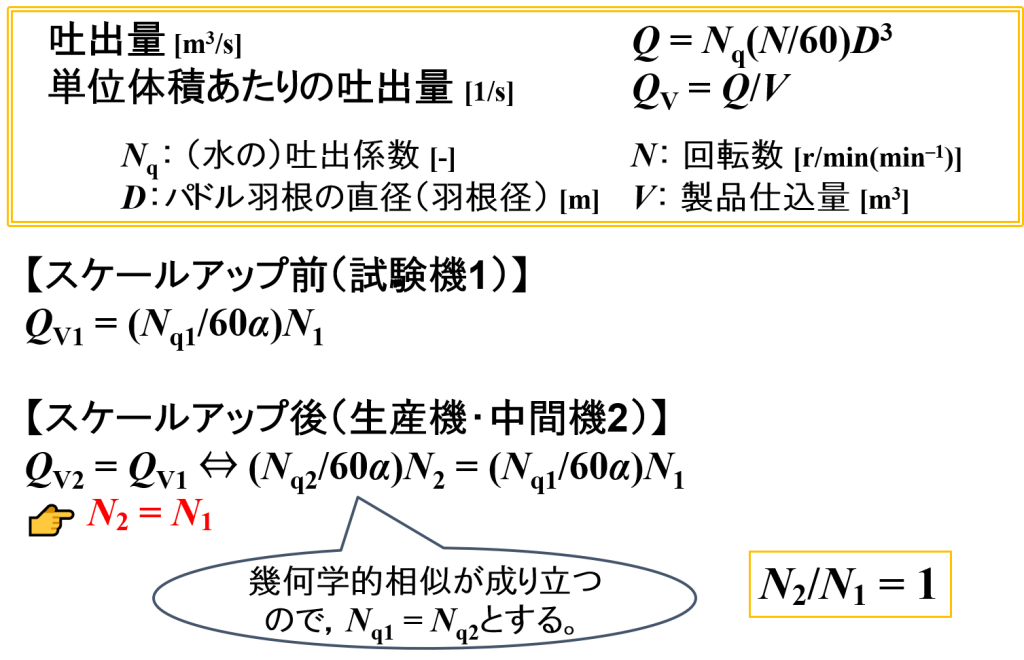
このときの回転数N₁，パドルミキサーの直径D₁とすると，単位体積あたりの吐出量は「Q_V1 = (N_q1/60α)N₁」となります。

スケールアップ後

このときの回転数N₂，パドルミキサーの直径D₂とすると，単位体積あたりの吐出量は「Q_V2 = (N_q2/60α)N₂」となります。

“単位体積あたりの吐出量一定”であるため，「Q_V2 = Q_V1」となります。

また，幾何学的相似が成り立つので「N_q1 = N_q2」とします。

そして，式変形をしていくと「N₂ = N₁」となります。

回転数Nを左辺に移項すると「N₂/N₁ = 1」が得られます。

📝[memo]　Q_V2 = Q_V1　⇔　(N_q2/60α)N₂ = (N_q1/60α)N₁　⇔　N₂ = N₁　⇔　N₂/N₁ = 1

単位体積あたりの吐出量一定時における撹拌作用の関係

“微細化作用He”と“吐出作用Q”を回転数Nとパドルミキサーの直径Dで表現することを考えます。

「スケールアップ理論を考えてみようー乳化編【周先端速度一定時における撹拌作用の変化】」のページで紹介したように，微細化作用Heと吐出量Qは次のように表されます。

• He ∝ N²D²
• Q ∝ ND³

単位体積あたりの吐出量が一定のとき，これらの撹拌作用がどのように変化するでしょうか？

微細化作用の関係

スケールアップ後の回転数N₂ = N₁で表されると紹介しました。

ここで，スケールアップ前後の微細化作用Heを計算します。

• スケールアップ前　👉　He₁ ∝ N₁²D₁²
• スケールアップ後　👉　He₂ ∝ N₂²D₂² = N₁²D₂²

He₂/He₁ ∝ N₁²D₂²/N₁²D₁² = (D₂/D₁)²

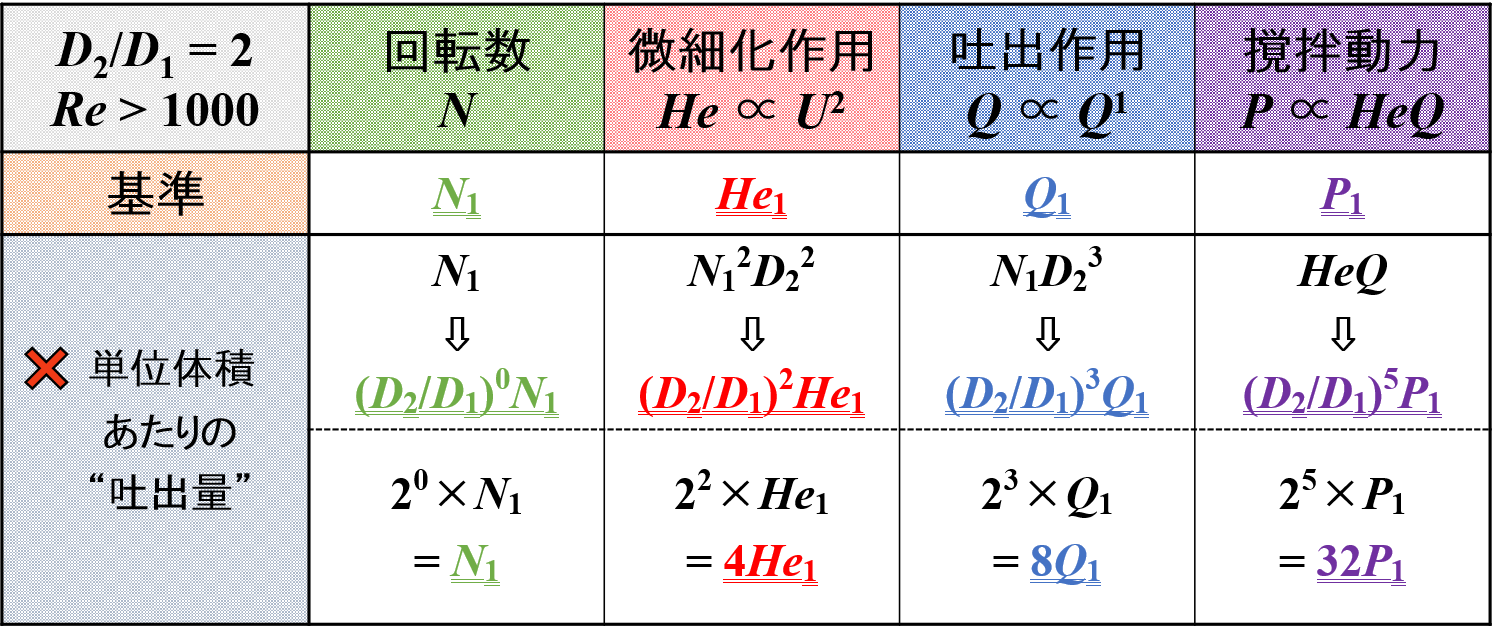
したがって，パドルミキサーの直径Dが2倍になると，微細化作用Heは4倍になることがわかります。

微細化作用を無視して吐出作用のみの条件を考えましたが，微細化作用が大きくなってしましました。

📝[memo]　パドルミキサーの直径Dの変化の仕方（スケールアップの仕方）によって，微細化作用Heは異なります（＝一定ではありません）。

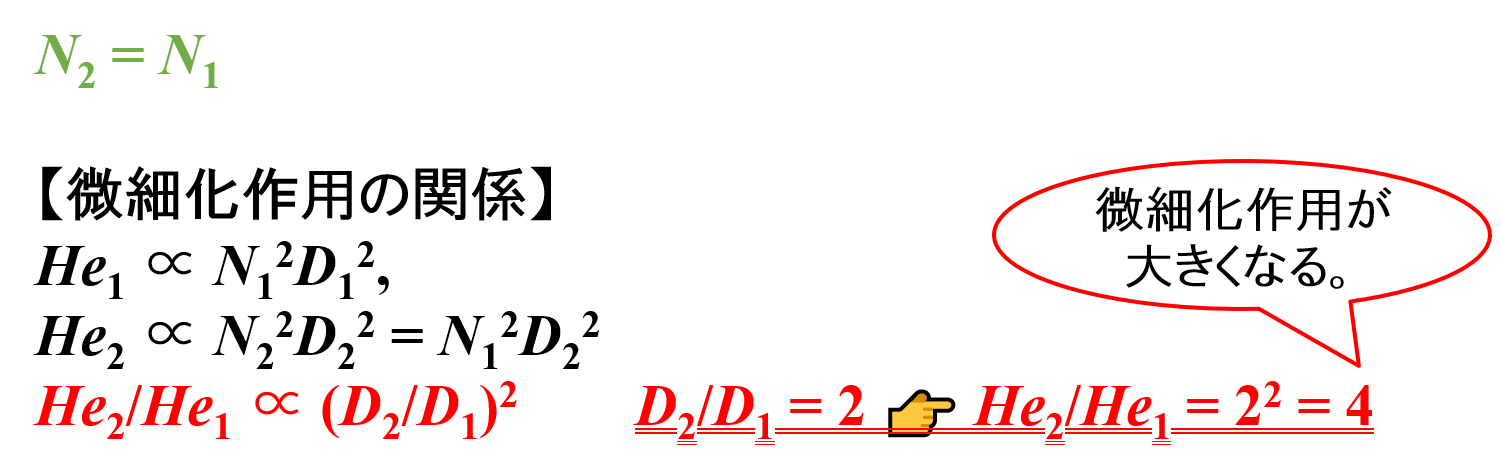
吐出作用の関係

次に，スケールアップ前後の吐出作用Qを計算します。

• スケールアップ前　👉　Q₁ ∝ N₁D₁³
• スケールアップ後　👉　Q₂ ∝ N₂D₂³ = N₁D₂³

Q₂/Q₁ ∝ N₁D₂³/N₁D₁³ = (D₂/D₁)³ = (V₂/V₁)

したがって，パドルミキサーの直径Dが2倍になると，吐出作用Qは8倍になることがわかります。

ただし，吐出作用Qは体積（V = αD³）に比例するので，単位体積あたりの吐出量Q_Vは一定になります。

📝[memo]　パドルミキサーの直径Dの変化の仕方（スケールアップの仕方）によって，吐出作用Qは異なります（＝一定ではありません）。

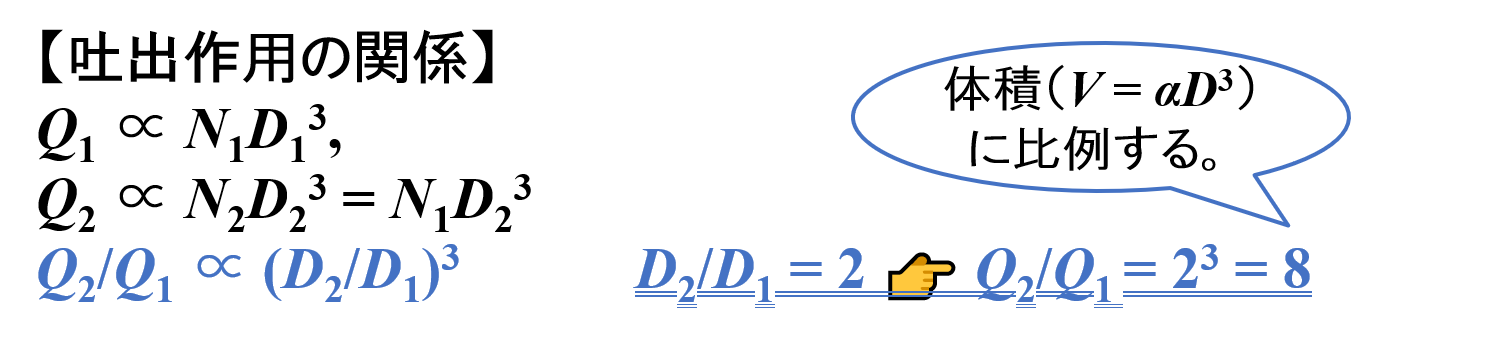
撹拌時間の関係

最後に，「”（条件②）パス回数が等しくなるようにする”という考え方」を採用して，撹拌作用ではありませんが撹拌時間についても考えます。

n₂ = n₁が成り立つ条件を採用することを意味します。

📝[memo]　「スケールアップ理論を考えてみようー乳化編【パス回数が等しくなるようにする】」のページで紹介しました。

また，「スケールアップ理論を考えてみよう ー 乳化編【“N^3D^2”とは？】」のページで紹介したように，幾何学的相似が成り立つのでV = αD³を満たします。

• スケールアップ前　👉　t₁ ∝ n₁V₁/Q₁ ∝ n₁(αD₁³)/(N₁D₁³) = αn₁/N₁
• スケールアップ後　👉　t₂ ∝ n₂V₂/Q₂ ∝ n₁(αD₂³)/(N₁D₂³) = αn₁/N₁

📝[memo]　パス回数の式を変形した乳化時間t = …の式に，上述した吐出量（吐出作用）Qを代入しています。

📝[memo]　ここでは「パス回数＝循環回数」，「乳化時間＝撹拌時間」と置き換えます。

t₂/t₁ ∝ (αn₁/N₁)/(αn₁/N₁) = 1

したがって，パドルミキサーの直径Dが2倍になっても，撹拌時間tは一定であることがわかります。

📝[memo]　パドルミキサーの直径Dがどのような変化（どのようなスケールアップ）をしても，撹拌時間tは一定になります。

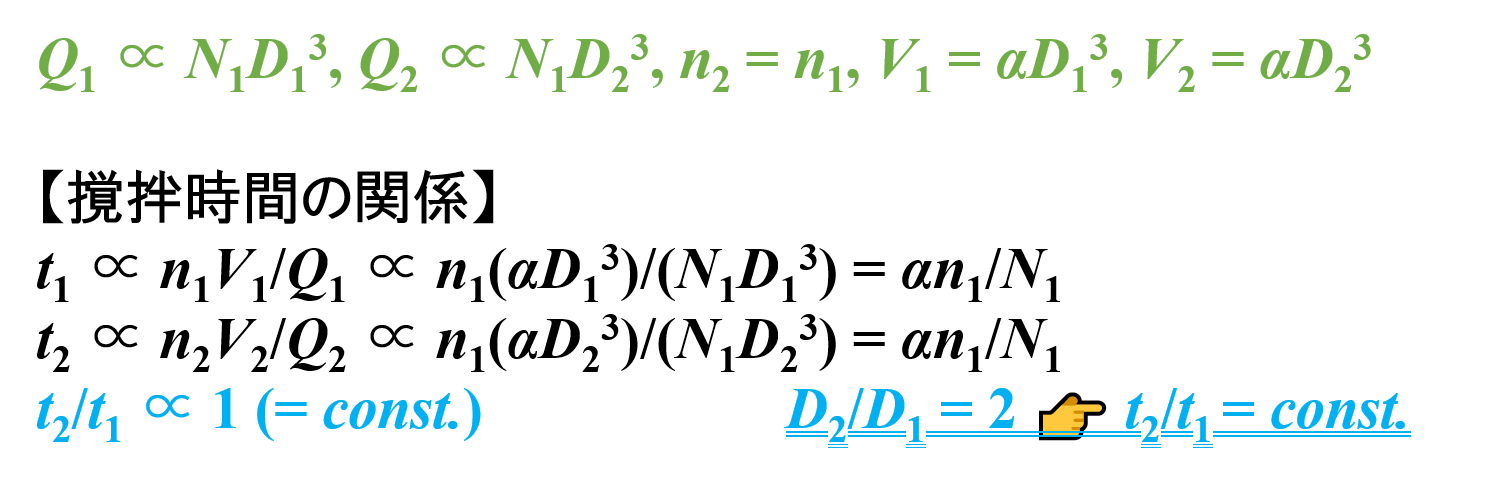
単位体積あたりの吐出量一定という条件は，撹拌時間一定と言い換えて理解しても良さそうです。

📝[memo]　この方が直感的にわかりやすいですね。

---

一方，「スケールアップ理論を考えてみよう ー 乳化編【回転数・混合時間/乳化時間の考え方】」のページで紹介した”無次元混合時間”を採用する場合があります。

• スケールアップ前　👉　t_M1 ∝ 1/N₁
• スケールアップ後　👉　t_M2 ∝ 1/N₂ = 1/N₁

📝[memo]　無次元混合時間の式を変形した混合時間t_M = …の式に，上述した回転数Nを代入しています。

📝[memo]　ここでは「撹拌時間＝混合時間」と置き換えます。

t_M2/t_M1 ∝ (1/N₁)/(1/N₁) = 1

したがって，タービン羽根の直径Dが2倍になっても，撹拌時間tは一定であることがわかります。

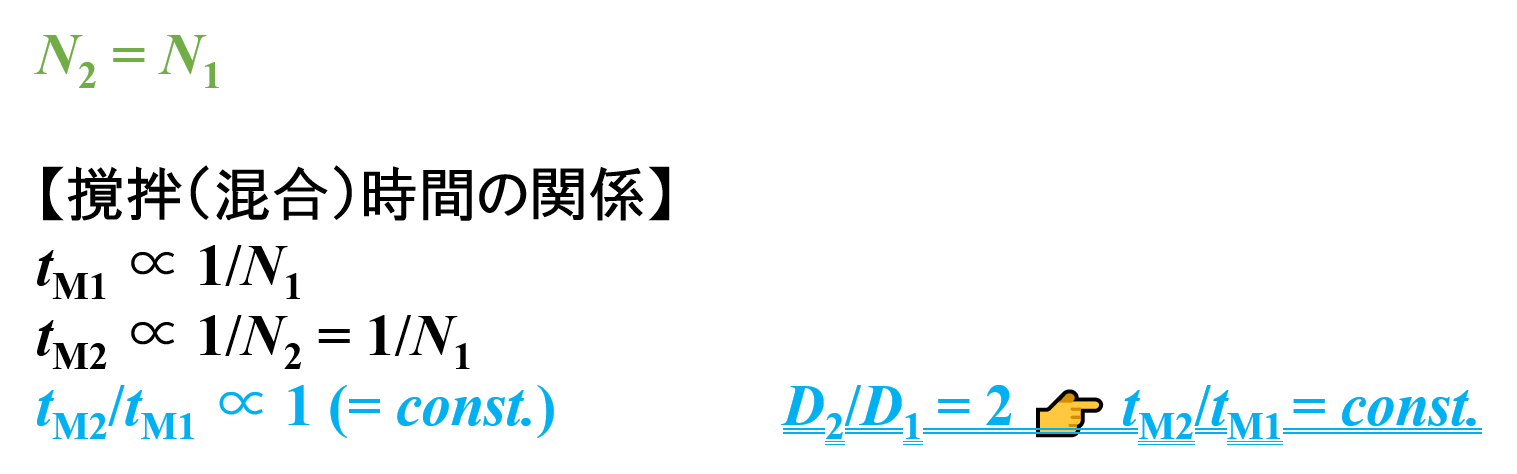
まとめ

ここで，まとめをしておきましょう。

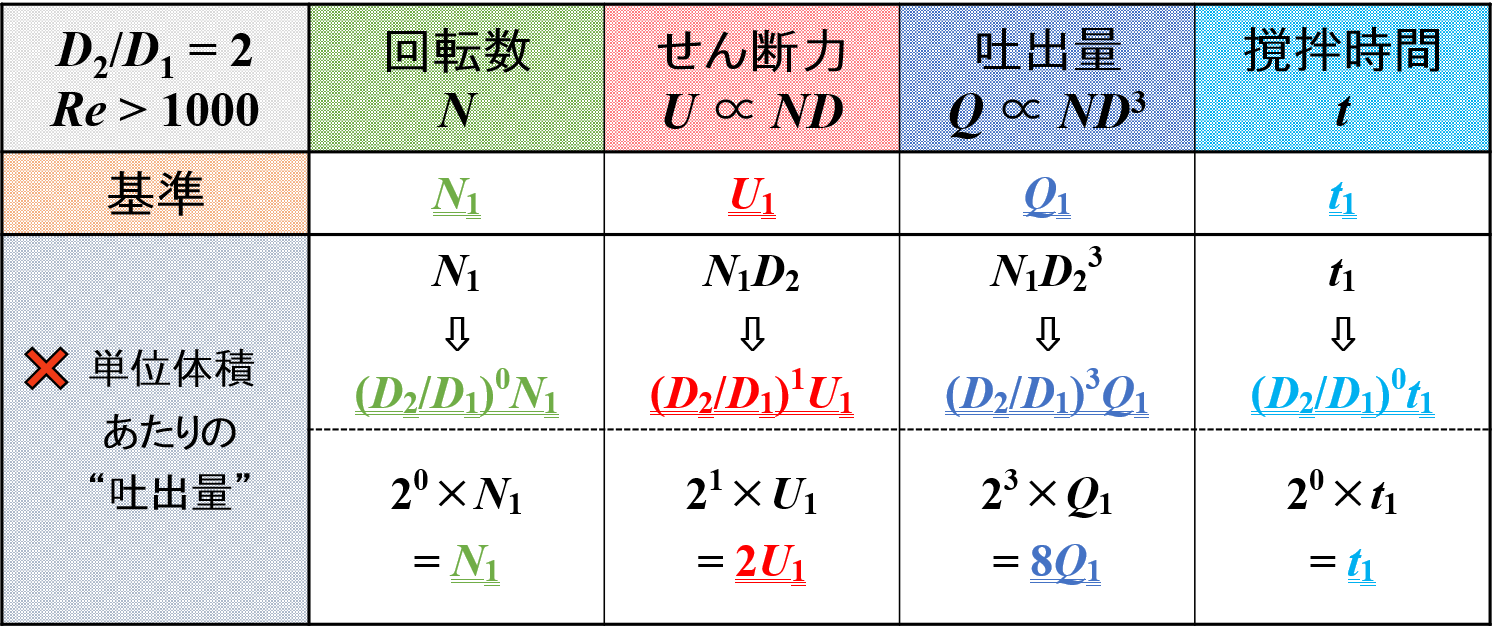
スケールアップをして羽根径が2倍になると，単位体積あたりの吐出量一定時において各種因子は下表のように変化します。

“回転数一定”であること

”単位体積あたりの吐出量一定”というのは，”回転数一定”ということを意味します。

しかしながら，乳化撹拌装置が大きくなったときに，試験機と同じホモミキサーの回転数・乳化時間を設定するのは困難です。

「スケールアップ理論を考えてみよう ー 乳化編【スケールアップによる製造規模の変更】」のページで紹介したように，大きな撹拌羽根を高速で回転させるためには，非常に大きなモータを必要とします。

モータが大きくなると高コストになりますが，モータを設置するフレームや，フレームを昇降するための油圧シリンダーも高コストになります。

したがって，実務では経済性の問題から採用できないという事情があります。

…ということは，”単位体積あたりの吐出量一定”というスケールアップ理論は扱うことができません。

ここまで読んでいただいた方には申し訳ありませんが，実際には適用できないダメな事例を長々と説明させていただきました。