吐出量の式

引き続き，「スケールアップ理論を考えてみよう ー 乳化編【ホモミキサーによる微細化作用とスケールアップ計算式】」で紹介した”（条件②）パス回数が等しくなるようにする”の考え方に着目します。

吐出量の式は下式の通りでした。

吐出量の意味

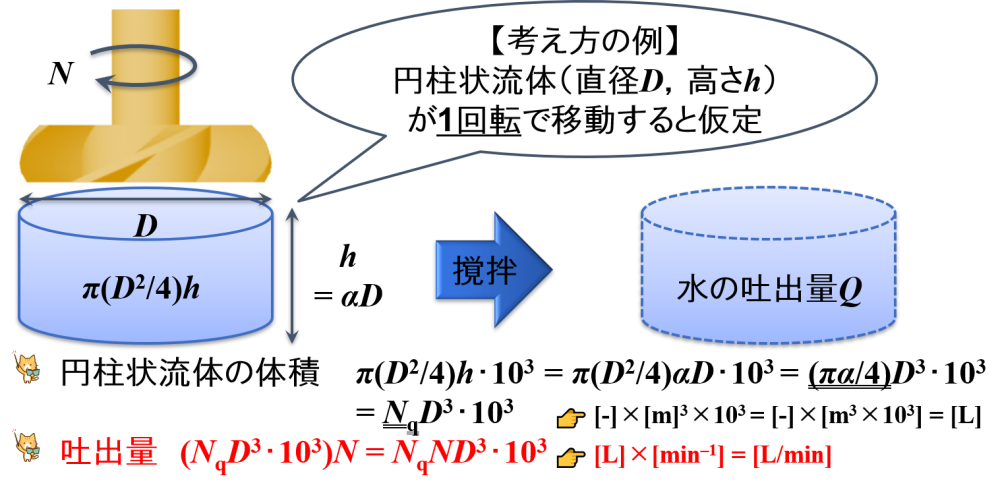
吐出量とは，撹拌羽根（今回の場合はタービン羽根）によって流体が移動する「量」を言います。

ここで，式の成り立ちについて簡単に確認しておきます。

考え方はいろいろありますが，円柱状流体（直径D/高さh）が移動すると仮定します。

ただし，高さh = αD（比例定数α）とします。

円柱状流体の体積　π(D²/4)h・10³ = π(D²/4)αD・10³ = (πα/4)D³・10³ = N_qD³・10³

👉　[-]×[m]³×10³ = [-]×[m³×10³] = [L]

円柱の体積を求める公式そのものです。

撹拌羽根が1回転するとき，この円柱状流体が移動します。

尚，πα/4は定数であるので，まとめてN_qに置き換えています。

吐出量　(N_qD³・10³)N = N_qND³・10³　👉　[L]×[min^–1] = [L/min]

1分間に回転する回数が回転数です。

そのため，吐出量（1分間に流体が移動する量）は「円柱状流体の体積」×「回転数」で得られます。

“分裂確率”と“吐出量”

「スケールアップ理論を考えてみよう ー 乳化編【高速撹拌機による液滴の微細化】」のページで紹介した“分裂確率”を絡めて，吐出量を考えたいと思います。

📝[memo]　難しいと思われた方は，分裂確率の概念は飛ばしてしまいましょう。

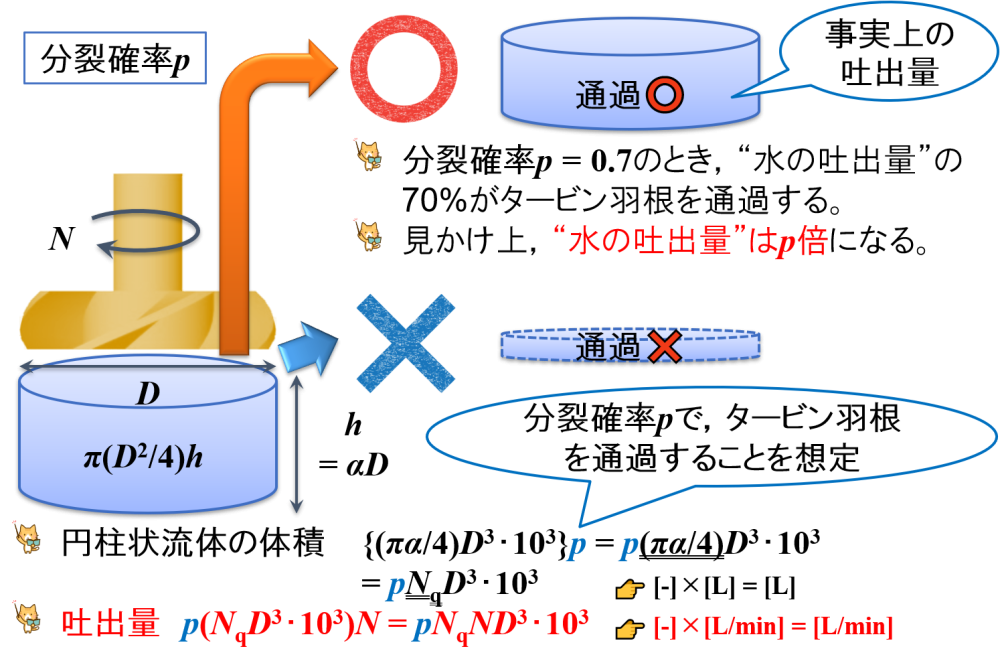
分裂確率が70%であるとき，タービン羽根を通過する“水の吐出量”が70%であると考えることができます。

そして，この70%の“水の吐出量”が，確実にタービン羽根を通過すると解釈することにします。

これが，事実上の吐出量に相当します。

そこで，上述した円柱状流体の体積を計算する段階で，このような分裂確率pの考え方を導入するとどうなるでしょうか？

円柱状流体の体積　{(πα/4)D³・10³}p = p(πα/4)D³・10³ = pN_qD³・10³　👉　[-]×[L] = [L]

吐出量は，上述した考え方で算出することができます。

このように考えると，事実上の吐出量を用いて正確に計算することができます。

一方で，基本的にスケールアップ前後で分裂確率は一定として扱うことにします。

スケールアップ前後で変化しない分裂確率をわざわざ考える必要はないので，これを無視することができます。

一方で，”従来の吐出係数N_q”から”新たな吐出係数pN_q”として考えることもできます。

分裂確率を無視すると，”従来の吐出係数N_q”をそのまま使用することを意味します。

”従来の吐出係数N_q”をそのまま使用しても良いか？という論点がありますが，この件については後述したいと思います。

後ほど，水の吐出係数N_qをそのまま使用しても良いか否かの議論が出てきますが，論点としては同じになります。

📝[memo]　ここでは“分裂確率”を取り上げましたが，結局は使わないことになりました。

しかしながら，実際にスケールアップをしてみると，理論上の乳化時間と実際に必要な乳化時間が異なることがあります。

これは，スケールアップ前後で分裂確率が変化している可能性があります。

📝[memo]　分裂確率 → 吐出量 → パス回数 → 乳化時間というように，密接に関連しています。

例えば粘度が高い製品になると，スケールアップ後の大型の乳化槽ではホモミキサー近傍でしか対流が起こらず，結果として分裂確率が低下することがあり得ます。

このような状況を想定して事前に吐出量を計算したいところですが，各製品の物性によって分裂確率が異なります。

例えば，製品Aはスケールアップ前後で分裂確率が一定でしたが，製品Bはスケールアップ後に分裂確率が20%減みたいなことがあるかもしれません。

したがって，製品Bをスケールアップするときはスケールアップ後の理論計算の結果を補正して，乳化時間を少し長くすることをする必要があります。

しかしながら，あらかじめ，このような補正をすることは難しいことだと思います。

製品を製造する各メーカーが実績や経験によってデータを蓄積していくことで，このような補正ができるだけの技術・ノウハウを身に着けていくことになります。

吐出量を決める因子

次に，吐出量の式に着目します。

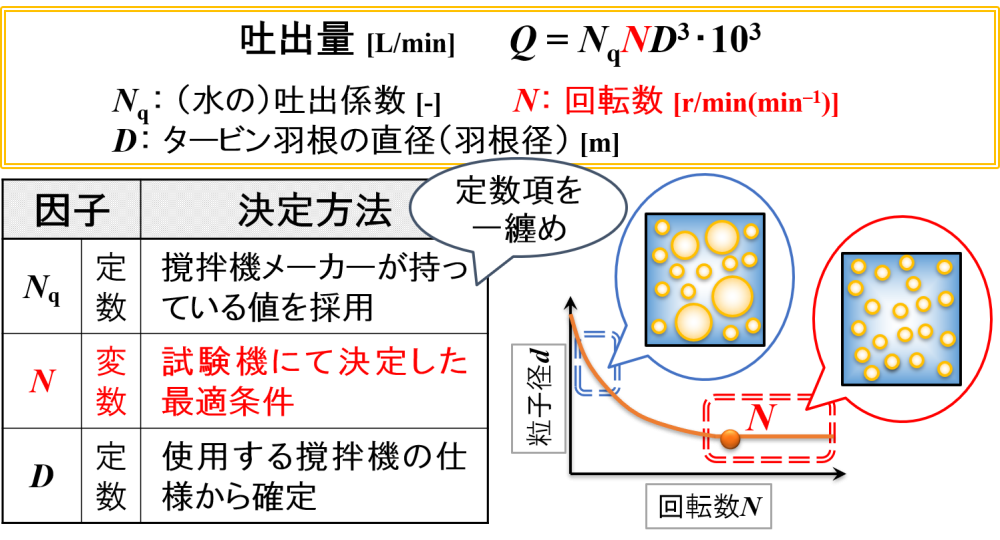
吐出量Qは，吐出係数N_q，回転数N，タービン羽根の直径Dによって決まります。

吐出係数N_q　👉　定数

撹拌機メーカーが持っている値になります。

回転数N　👉　変数

試験機にて決定した最適条件によって決まるものです。

回転数Nと粒子径dの関係を調べ，これ以上回転数Nを高くしても粒子径dが小さくならない値を調べます。

「スケールアップ理論を考えてみよう ー 乳化編【周先端速度が等しくなるようにする】」のページで，周先端速度Uを求めるために同じことを検討しました。

タービン羽根の直径D　👉　定数

使用するホモミキサーが決まっているので，自然に決定する値です。

このように考えると，最適な回転数Nさえ決めてしまえば，吐出量Qは計算によって求められることがわかります。

“パス回数nが等しくなるようにする”条件（＝パス回数の式）を採用するため，あらかじめ吐出量Qを算出しておきます。

具体的な計算については，「スケールアップ理論を考えてみよう ー 乳化編【スケールアップの検討例①】」のページで紹介します。

実際の製品に対する吐出係数の考慮

上述したように，吐出量の式からホモミキサーによる吐出量を計算することができます。

このとき，吐出係数N_qを用いるのですが，厳密には水の吐出係数 N_qを意味します。

実際には製品を取り扱うことになるので，製品の吐出係数を使用すべきと考えます。

そのため，吐出量を計算するのあたって，水の吐出係数 N_qをそのまま使用しても良いか否かの議論が必要です。

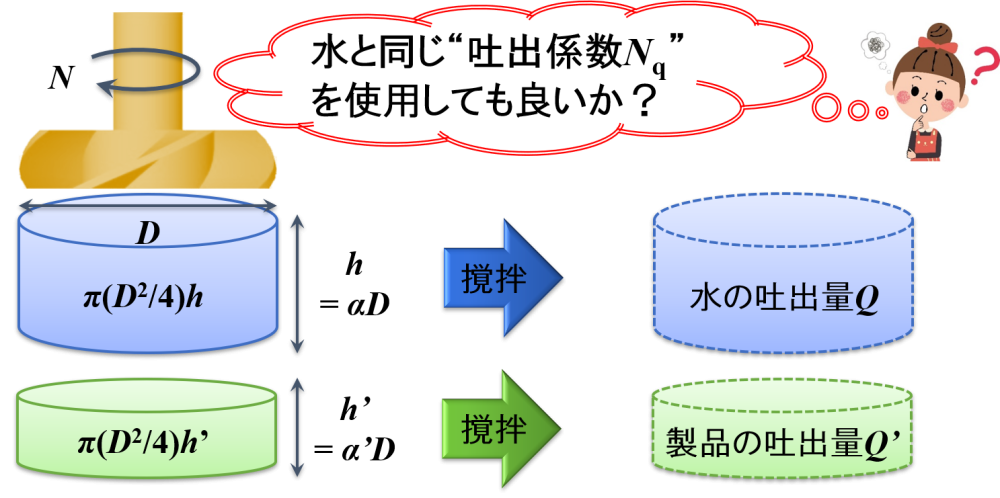
製品の吐出係数

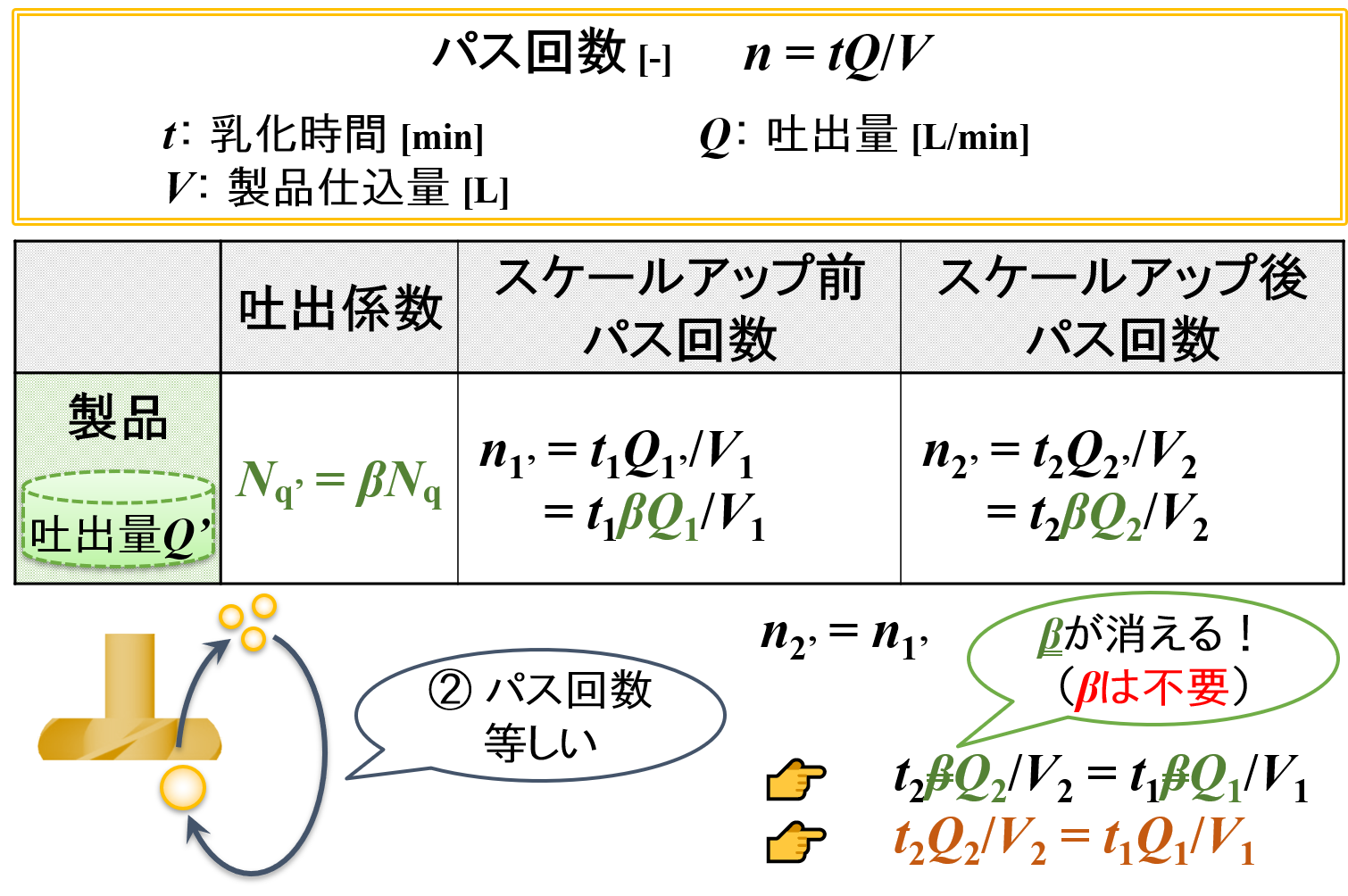
そこで，製品の吐出係数N_q’を規定し，水の吐出係数 N_qのβ倍であるとします。

すなわち，N_q’ = βN_qとなります。

このとき，水と製品におけるスケールアップ前後の吐出量Qを計算します。

📝[memo]　同一の製品であれば，βは一定で変化しないと考えます。

水

• スケールアップ前　👉　Q₁ = N_q1N₁D₁³・10³
• スケールアップ後　👉　Q₂ = N_q2N₂D₂³・10³

製品

• スケールアップ前　👉　Q_1′ = N_q1′N₁D₁³・10³ = βN_q1N₁D₁³・10³ = βQ₁
• スケールアップ後　👉　Q_2′ = βQ₂（Q_1′と同じ算出方法）

製品のパス回数が等しくなるようにする

続いて，製品におけるスケールアップ前後のパス回数nを計算します。

• スケールアップ前　👉　n_1’ = t₁Q_1’/V₁ = t₁βQ₁/V₁
• スケールアップ後　👉　n_2’ = t₂βQ₂/V₂（n_1′と同じ算出方法）

そして，「スケールアップ理論を考えてみようー乳化編【パス回数が等しくなるようにする】」のページで紹介した考え方から，スケールアップ前後のパス回数が等しくなるようにします。

n_2′ = n_1′　⇔　t₂βQ₂/V₂ = t₁βQ₁/V₁　⇔　t₂Q₂/V₂ = t₁Q₁/V₁

途中で両辺に同じβが存在するので，このβを消すことができます。

その結果，「スケールアップ理論を考えてみようー乳化編【パス回数が等しくなるようにする】」のページで紹介した“パス回数一定”の一般式としての表し方と同じ形が現れます。

📝[memo]　実際には「t₂Q₂/V₂ = t₁Q₁/V₁　⇔　t₁Q₁/V₂ = t₂Q₂/V₂」の変形が必要ですね。

したがって，実際の製品に関係なく水と同じ吐出係数N_qを用いて良いという結論が得られます。