ホモミキサーによるせん断モデル

「スケールアップ理論を考えてみよう ー 乳化編【ホモミキサーによる微細化作用とスケールアップ計算式】」のページでホモミキサーについて振り返りましたが，もう一度振り返っておきましょう。

ホモミキサーは固定化されて動かない部品「ケーシング」と高速で回転する「タービン羽根」から構成されており，粒子がタービン羽根を通過すると微細化作用が働きます。

スケールアップ時におけるホモミキサーによる微細化作用は，“せん断力”のみによって働くと考えることにしました。

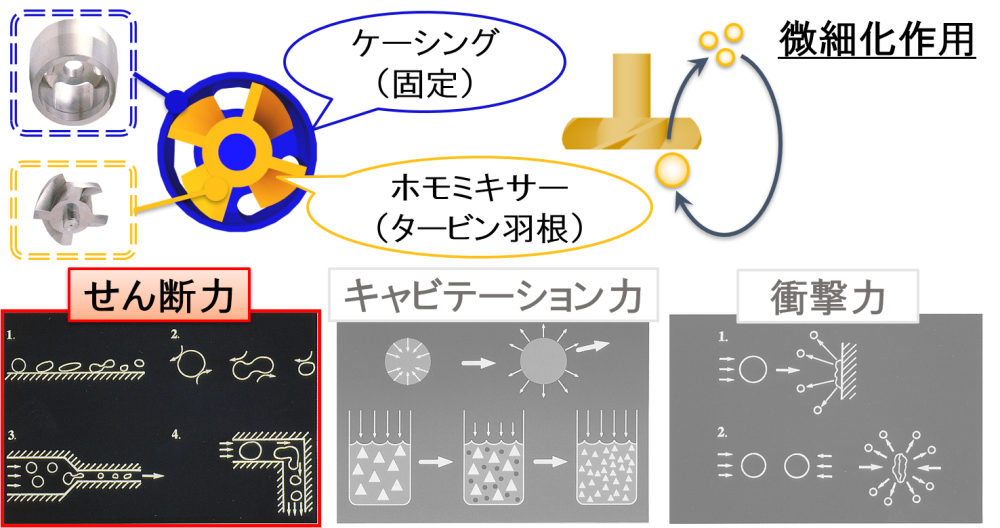
ホモミキサーによって液滴の微細化が起こるメカニズム

このようなホモミキサーの構造を踏まえて，ホモミキサーによるせん断モデルを次のように考えます。

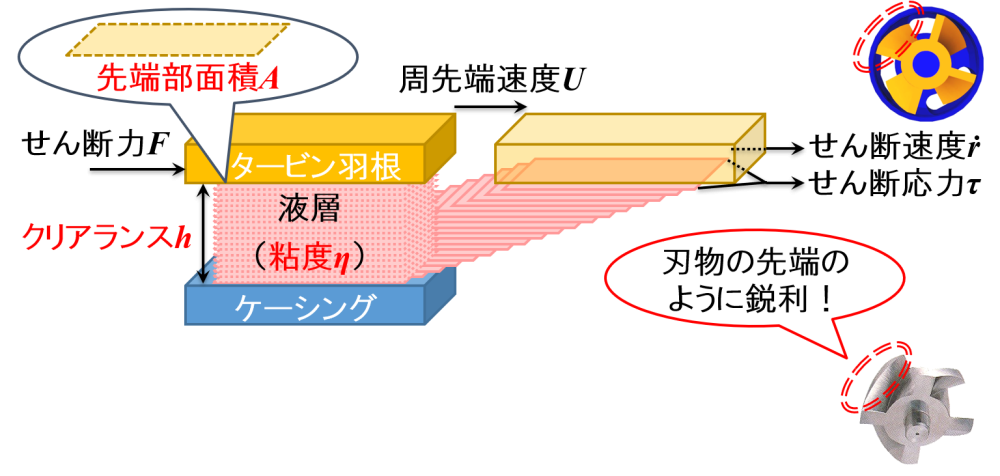
① ホモミキサーを通過する粘度ηの流体は，固定化されて動かない部品「ケーシング」と高速で回転する「タービン羽根」の間（クリアランスh）で液層となります。

📝[memo]　「スケールアップでエマルションを評価しよう【粘度の定義】」のページで紹介したように，このモデルでは粘度を取り扱うために敢えて液層と表現しています。

② タービン羽根が回転して周先端速度Uで動くとき，タービン羽根（先端部面積A）に接する液層に対してせん断力Fが働きます。

③ その結果，高さhの位置にある液層はせん断速度ṙで動き，その断面にせん断応力τが生じます。

📝[memo]　液層が受けるせん断応力については後述します。

このようなプロセスで，ホモミキサーによって液滴が微細化されるとして考えましょう。

スケールアップで自然に守られる3つの条件とは？

スケールアップの目的でホモミキサーを使用すると自然に守られる条件があり，スケールアップ前後で等しくなるようになっています。

ここでは，ホモミキサーによるせん断力に起因する3つの条件について考えます。

クリアランスh

当社のようにホモミキサーを取り扱うメーカーでは，どのような大きさのホモミキサーであっても，最小となるクリアランスhが等しくなるように製作しています。

したがって，クリアランスhは常に一定でありスケールアップ前後で変化しません。

基本的に，クリアランスhは小さい方が好ましいです。

その理由は，液滴を微細化するために大きな速度差を生じやすくなるので，せん断力によって小さな液滴を生成することができます。

また，「スケールアップでエマルションを評価しよう【エマルションの粘度特性①】」のページで紹介したように，エマルションは準（擬）塑性流体に該当します。

クリアランスhを小さくして大きなせん断力を付与することによって，エマルションを効率よく流動させることができます。

タービン羽根先端部面積A

タービン羽根の先端は，刃物のように鋭利な状態です。

この部分の面積（タービン羽根先端部面積A）は非常に小さいため，タービン羽根の大きさによってほとんど変わらないと考えます。

したがって，タービン羽根先端部面積Aは常に一定でありスケールアップ前後で変化しないとみなします。

液層の粘度η

通常，乳化をするときホモミキサーを使用します。

処方が変わらないのであれば，乳化をするときの分散液の物性はスケールに関係なく同じであるはずです。

したがって，液層の粘度ηは常に一定でありスケールアップ前後で変化しません。

せん断力と周先端速度の関係

上述したホモミキサーによるせん断モデルから，実際のせん断力の大きさを計算してみましょう。

ここで，「スケールアップでエマルションを評価しよう【粘度の定義】」のページで紹介した粘度の式を使います。

「η = Fh/AU」の式は，「F = UAη/h」の式に変形することができます。

そしてホモミキサーによるせん断モデルに合わせて粘度の式におけるインデックスを変更します。

• 液層を動かす力F　👉　せん断力F
• 液層の高さh　👉　クリアランスh
• 液層が動く速度U　👉　周先端速度U
• 液層断面積A　👉　先端部面積A

📝[memo]　粘度ηはそのままとします。

すると，「F = UAη/h」の式はホモミキサーによって付与するせん断力Fを意味することがわかります。

そこで，この式とスケールアップで自然に守られる3つの条件について考えます。

📝[memo]　せん断応力については一旦無視しましょう。

スケールアップで自然に守られる3つの条件とせん断力

ここで，スケールアップで自然に守られる3つの条件を振り返ってみましょう。

クリアランスh，タービン羽根先端部面積A，液層の粘度ηはスケールアップ前後で変化しませんでした。

…ということは，スケールアップ前後で変化しない値について，わざわざ検討する必要はありません。

「F = UAη/h」の式に着目すると，「クリアランスh，タービン羽根先端部面積A，液層の粘度η」は無視することができるため，「F ∝ U」とみなすことができます。

すなわち，せん断力Fは周先端速度Uのみを考えれば良いという結論が得られます。

また，せん断応力を表す式「τ = F/A」について考えると，タービン羽根先端部面積Aは無視できるので，「τ ∝ F」とみなすことができます。

したがって，ホモミキサーが付与するせん断力Fが等しければ，液層が受けるせん断応力τも等しくなることがわかります。

📝[memo]　イメージではこのような解釈でも問題ないですが不正確な面を含むので，この後に少し細かい説明をします。

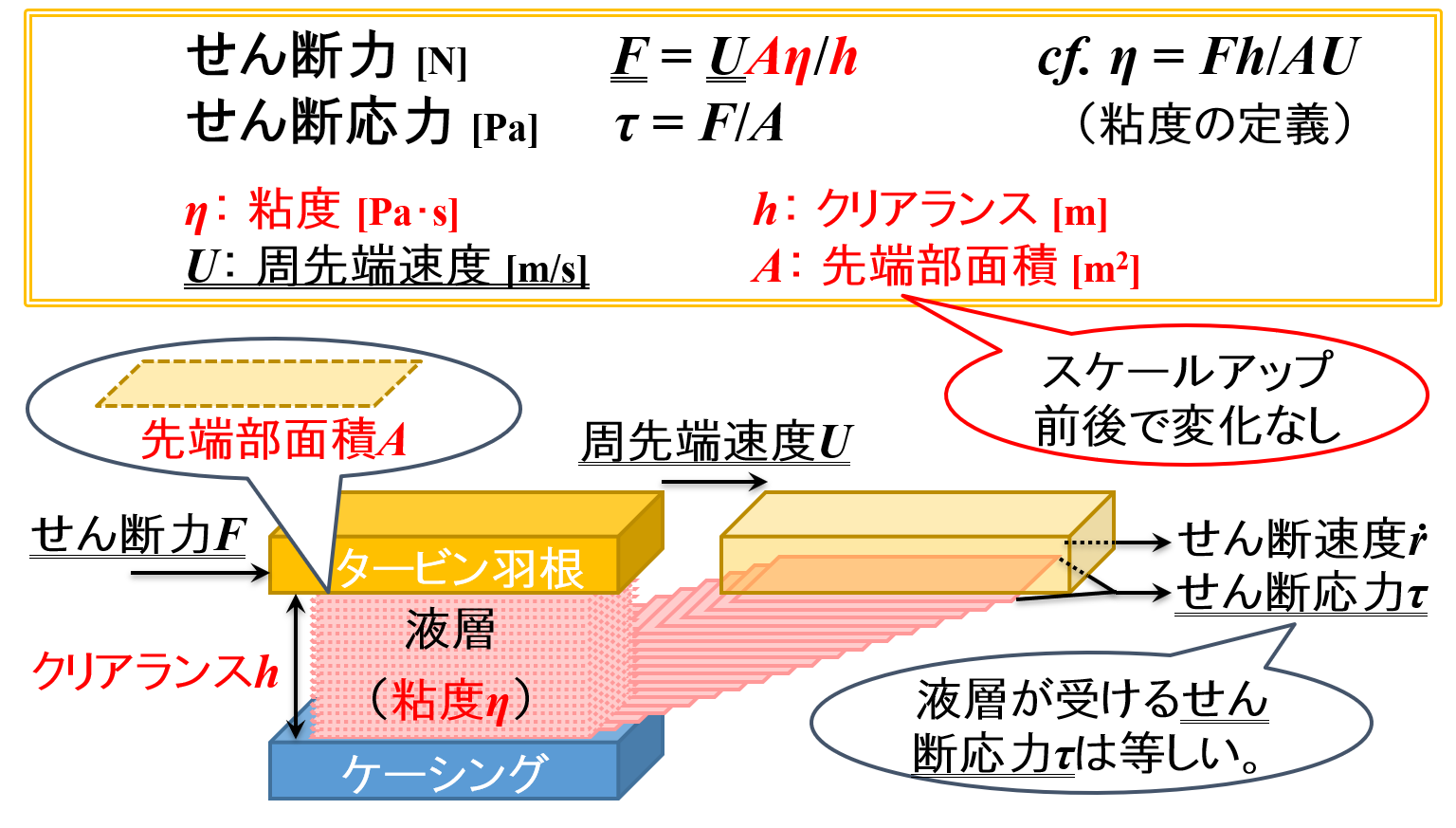
液層が受けるせん断応力τ

せん断応力τについて，少し細かい説明をしておこうかと思います。

難しいなと思われた方は読み飛ばしていただいても問題ありません。

流体は準（擬）塑性流体に該当するエマルションを想定しています。

タービン羽根に近い液層は大きな速度差を生じるので，大きなせん断応力τを受けることがわかります。

一方，ケーシングに近い液層は速度差が小さくなるので，小さなせん断応力τを受けることがわかります。

このように考えると，液層の位置（高さ）によって受けるせん断応力τの大きさが異なります。

📝[memo]　準（擬）塑性流体なので，液層の位置（高さ）によって流動性も異なります。

スケールアップ前後においては，クリアランスhと液層の粘度ηは変化せず一定でした。

すなわち，液層は同じように変形します。

したがって，液層の各高さにおけるせん断応力τ（＝せん断応力τの分布）は等しいと考えることができます。

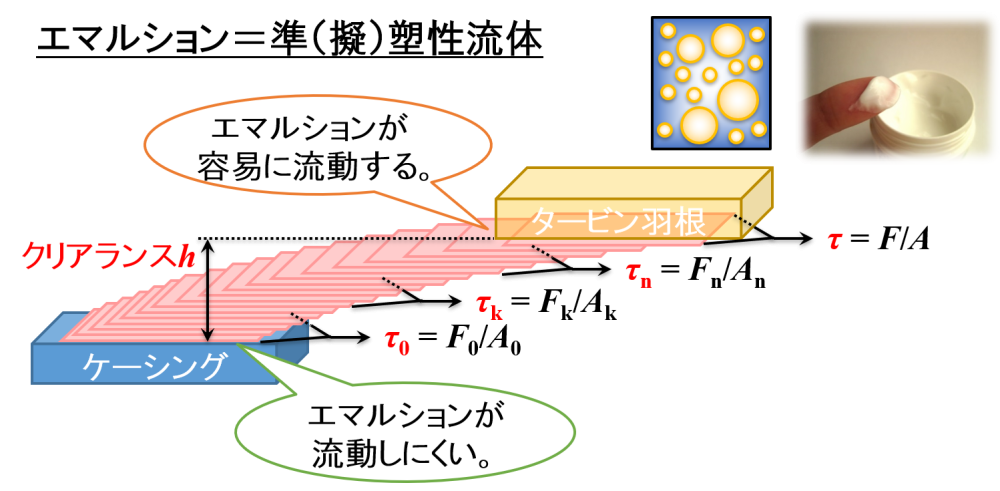
液層の位置（高さ）によって受けるせん断応力τの大きさが異なるので，いろいろな大きさの液滴が生成することが想像できます。

一方で，液滴は高速で回転する「タービン羽根」を複数回通過しています。（＝パス回数）

すると，一番大きなせん断応力τを受ける確率が高くなっていき，撹拌が十分であれば，いずれは一番大きなせん断応力τだけを受けているとみなしても良いことになります。

この考え方をもって，液層が受けるせん断応力τは等しいと解釈することにします。

そして，一番大きなせん断応力τを生じさせるのは，タービン羽根の周先端速度Uで液層が動くときです。

結果として，せん断応力τは周先端速度Uのみを考えれば良いという結論が得られます。

せん断力Fのときの考え方と同じ結論になったので，”せん断力”と”せん断応力”の違いは気にせずに進めることにしましょう。

📝[memo]　ホモミキサーが発揮する力（せん断力F）と液層が受ける力（せん断応力τ）は等しいとして考えていきましょう。ある意味，当たり前のことを言ってますよね。