撹拌装置で使用する撹拌機

乳化撹拌装置は乳化を利用したエマルション製品を製造することを主目的としています。

📝[memo]　高速撹拌機は乳化目的だけに限られることはないので，乳化以外の用途でも使用することができます。

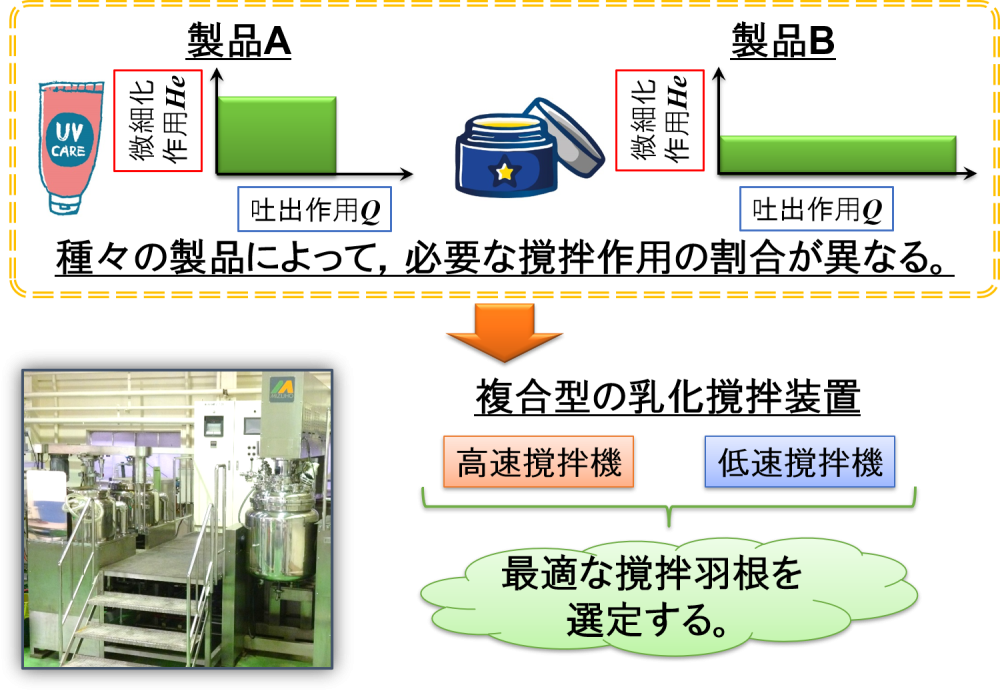
例えば，エマルション製品と一口に言っても，種々の製品が存在します。

そして，種々の製品によって，必要な撹拌作用（吐出作用と微細化作用）の割合が異なってきます。

乳化撹拌装置を使用する場合，微細化作用を有する高速撹拌機と吐出作用を有する低速撹拌機が備え付けられています。

このとき，乳化撹拌装置における最適な撹拌羽根を選定することが重要になります。

ここでは，乳化に限らず，撹拌装置で使用する撹拌機について見ていくことにしましょう。

乳化撹拌装置で使用する“高速撹拌機”

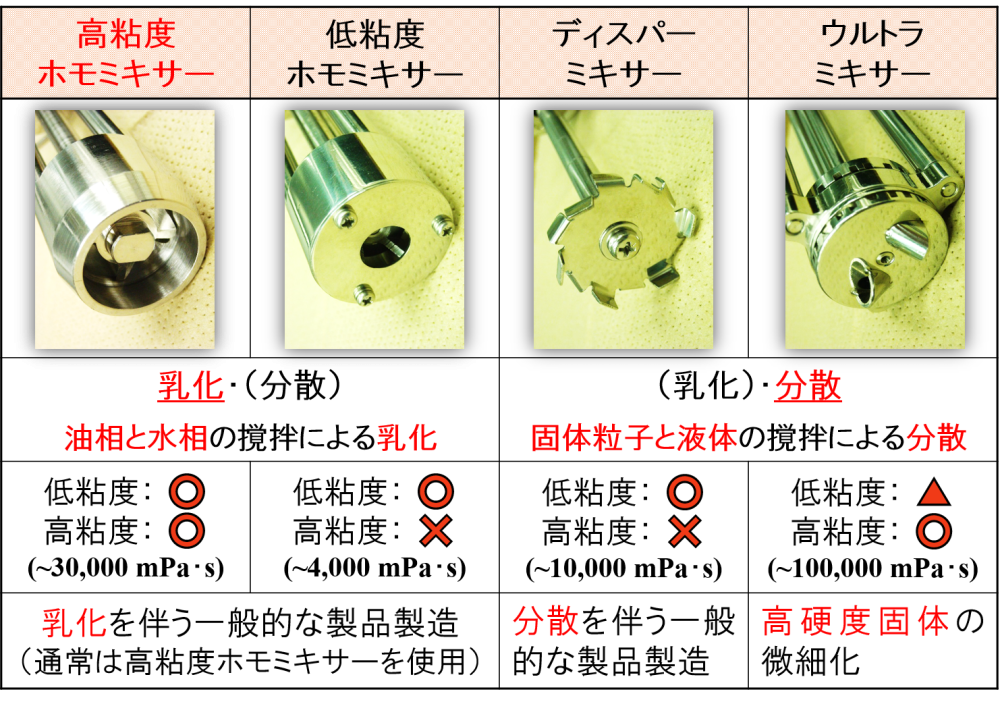
まずは，高速撹拌機を使用する用途として「乳化」と「分散」に分けたいと思います。

• 「乳化」は，液体中に液体が存在する状態を作り出すイメージです。
• 「分散」は，液体中に固体が存在する状態を作り出すイメージです。

乳化

一般的に高粘度ホモミキサーを使用します。

ホモミキサーで液体にせん断力を付与すると，速度差によって液体は容易に変形するので，比較的微細化されやすいと考えることができます。

昔は製品の粘度によって使い分けていましたが，現在では高粘度ホモミキサーに統一されつつあります。

高粘度ホモミキサーは低粘度ホモミキサーの使用領域をカバーできることが明らかになってきたため，低粘度ホモミキサーをわざわざ使用する機会が減ってきました。

📝[memo]　古くから低粘度ホモミキサーを使用してエマルション製品を製造されているメーカーでは，これまで実績のある撹拌機を変更したくないとの理由から，現在でも低粘度ホモミキサーを使用しています。

分散

一般的にディスパーミキサーを使用します。

固体は自由に変形することができないため，ディスパーミキサーの衝撃力によって微細化する方が好ましいと考えることができます。

ただし，高粘度製品になるとディスパーミキサーでは効果的な流動が得られません。

空回りのような状態が見られるようになります。

そのような場合は，みづほ工業独自の撹拌機である「ウルトラミキサー」を使用することがあります。

ウルトラミキサーは，高硬度固体を粉砕して微細化するのにも適しています。

「 高速撹拌機による流動状態」のページでも，これら”高速撹拌機”の説明をしています。

乳化撹拌装置で使用する“低速撹拌機”

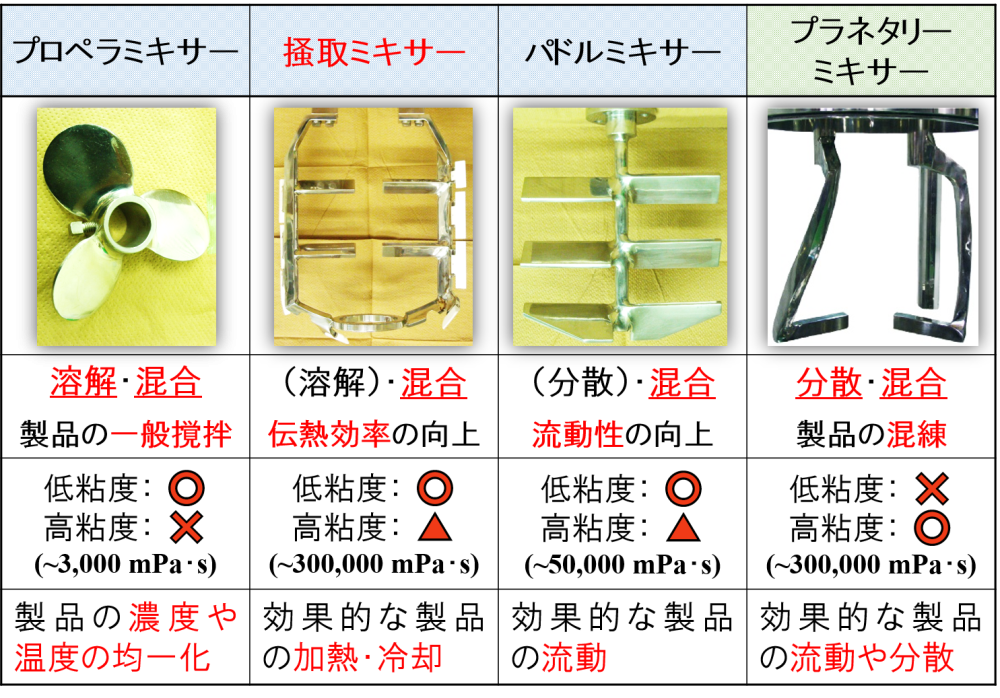
続いて，低速撹拌機を見ていきます。

ここでは，次の3つの使用方法に分けたいと思います。

主に単独で使用

プロペラミキサーが該当します。

上下に対流を引き起こすことができる撹拌羽根は多くないため，プロペラミキサーは優秀な撹拌羽根と言えます。

ただし， 高粘度製品になると効果的な流動性が得られません。

「撹拌をやさしく捉えてみよう【低速撹拌機と高速撹拌機】」のページで，その他特徴について説明しています。

主に他の撹拌羽根と併用して使用

掻取ミキサーが該当します。

高速撹拌機（ホモミキサー）と併用することが多いです。

撹拌羽根がタンクの壁面まで近づいているので，タンク壁面で熱交換をするような場合，効果的な製品の加熱・冷却に期待ができます。

また，パドルミキサーも該当します。

高速撹拌機（ホモミキサー）や掻取ミキサーと併用することが多いです。

これは撹拌機が追加されたことを意味するので，効果的な製品の流動に期待ができます。

📝[memo]　 低速撹拌機の数を増やして吐出作用を大きくします。

真空練合装置で使用

各種プラネタリーミキサーが該当します。

高粘度製品を対象とするので，低速撹拌機でありながら効果的な製品の流動と分散も期待ができます。

逆に，低粘度製品では効果がありません。

流動がほとんど見られません。

「撹拌をやさしく捉えてみよう【真空練合装置】」のページで，その他特徴について説明しています。

汎用的な各種撹拌羽根の動力特性

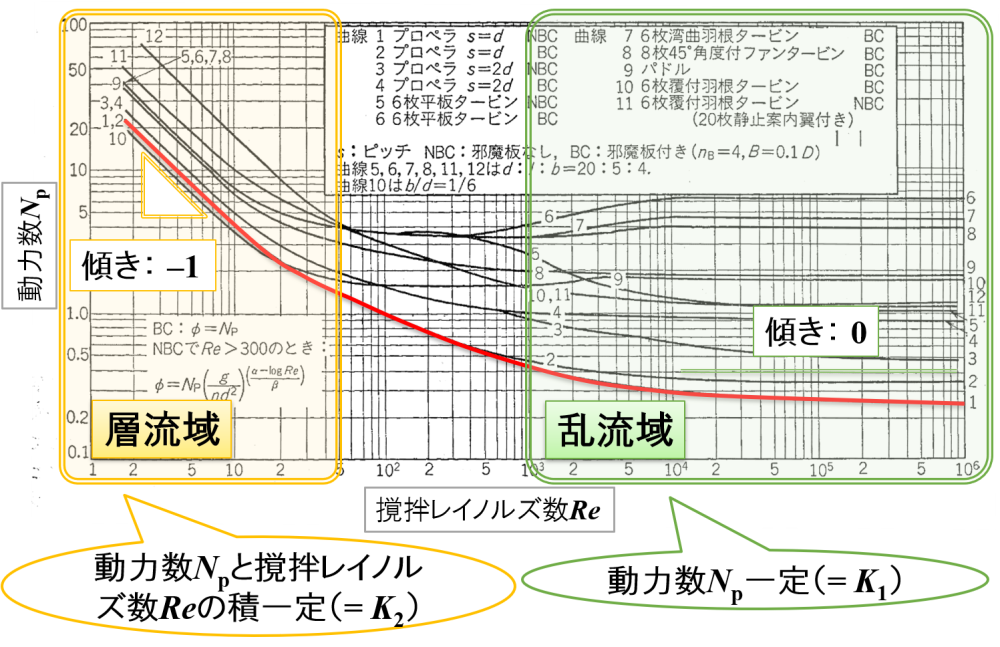
昔，様々な撹拌羽根を用いて，撹拌レイノルズ数と動力数の関係が調べられました。

下図はその結果になります。

ここでは，赤線で示したとある撹拌羽根に注目します。

📝[memo]　 どの撹拌羽根でも同じような傾向となるので問題ありません。

そして，層流域と乱流域における特徴について，撹拌レイノルズ数・動力数の式を変形して考えてみましょう。

📝[memo]　”対数”グラフによる表示になっている点に注意が必要です。

📝[memo]　内容が難しいと思われた方は，遠慮なく飛ばして次に行きましょう！

🚩 [引用：社団法人化学工学協会編『化学工学便覧』丸善，1988]

層流や乱流については，「撹拌をやさしく捉えてみよう【撹拌による槽内の流動】」のページで説明しています。

動力数・正味の所要動力とは…

初めて出てきた言葉になるので，簡単に紹介しておきたいと思います。

大前提として，”運動エネルギー”という概念があります。

これは，ニュートン力学において「物体の質量と速さの2乗に比例する」のですが，ここではそういうものとしてそのまま受け入れることにしましょう。

”運動エネルギー”は，「K = (1/2)mv²」という式で表されることが知られていますね。

このとき，「1秒間あたりの運動エネルギー」が「正味の所要動力」に相当します。

「製品に対して付与できる1秒間あたりの撹拌エネルギー」と捉えても良いかもしれません。

動力数の式を「P_net = N_pρN³D⁵」と変形しておきます。

「正味の所要動力P_net」は変数である「回転数N」の3乗と「撹拌羽根の代表直径D」の5乗に比例します。

ここで，上述した”運動エネルギー”を使ってイメージしておきたいと思います。

質量m＝密度ρ×体積V(∝ D³)なので，「m ∝ ρD³」とすることができます。

特に，撹拌羽根が質量mの流体を移動させるとき，その回転数Nがときは「m ∝ ρND³」となります。

📝[memo]　「スケールアップ理論を考えてみよう ー 乳化編【“ホモミキサー”による吐出量】」のページで説明しますが，移動させる流量（吐出量）は回転数Nに比例します。

また，「スケールアップ理論を考えてみよう ー 乳化編【周先端速度が等しくなるようにする】」のページで紹介しますが，周先端速度の考え方から「v ∝ ND」とすることができます。

すると”運動エネルギー”は，「K = (1/2)mv² ∝ (1/2)(ρND³)(ND)² = (1/2)ρN³D⁵」となります。

ところで，回転数Nは”1分間あたり”に回転する回数を意味することが多いです。

質量mを「m ∝ ρND³」と表現することによって，”1分間あたり”の値を意味することになります。

ここで，比例∝の概念を取り入れているので，”1分間あたり”を”1秒間あたり”と読み替えることができます。

したがって，上述した”運動エネルギー”を正確に表現すると，”1秒間あたりの運動エネルギー”となります。

📝[memo]　上式では，最初から”1秒間あたり”に回転する回数を書いています。

そして，正味の所要動力に置き換えると，「P_net = N_pρN³D⁵」となります。

このときの比例定数が「動力数N_p」に該当すると考えることができます。

📝[memo]　”1秒間あたりのエネルギー”と”動力”は，共に同じ単位系「W = J/s」を持ちます。

具体的な考え方は，「スケールアップ理論を考えてみよう ー 乳化編【“N₃D₂”とは？】」で改めて紹介します。

ここでは式変形をするだけの目的で使用します。 式の意味については深く考えなくても大丈夫です。

内容が難しいと思われた方は，遠慮なく飛ばして次に行きましょう！

乱流域

緑色の四角で囲まれた範囲が該当します。

理由は明らかではありませんが実験事実として，乱流域における曲線の傾き（接線）はおおよそ0とみなせることがわかりました。

すなわち，動力数N_pが一定であることを意味します。

そこで，この動力数N_pがK₁であると仮定します。

📝[memo]　logN_p = logK₁ ⇔ N_p = K₁

動力数の式を用いて「正味の所要動力P_net」を求めると，下図にようになります。

このとき，「回転数N」と「撹拌羽根の代表直径D」は撹拌機の条件（仕様）です。

製品の物性としては，その「密度ρ」が「正味の所要動力P_net」に影響を与えることがかります。

層流域

黄色の四角で囲まれた範囲が該当します。

理由は明らかではありませんが実験事実として，層流域における曲線の傾き（接線）はおおよそ「-1」とみなせることがかりました。

すなわち，「動力数N_p」と「撹拌レイノルズ数Re」の積が一定であることを意味します。

そこで，「動力数N_p」と「撹拌レイノルズ数Re」の積がK₂であると仮定します。

📝[memo]　logN_p = –logRe + logK₂ = log(1/Re) + logK₂ = log(K₂/Re) ⇔ N_p = K₂/Re ⇔ N_pRe = K₂

撹拌レイノルズ数と動力数の式を用いて「正味の所要動力P_net」を求めると，下図にようになります。

このとき，「回転数N」と「撹拌羽根の代表直径D」は撹拌機の条件（仕様）です。

製品の物性としては，その「粘度η」が「正味の所要動力P_net」に影響を与えることがかります。

---

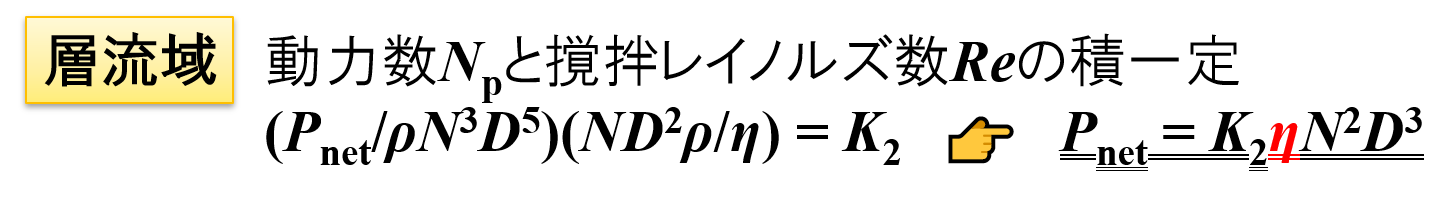
ここで，製品の物性のみに着目したいと思います。

必要とする「正味の所要動力P_net」は，製品の「密度ρ」と「粘度η」に依存することがわかりました。

すなわち，「製品に対して付与できる1秒間あたりの撹拌エネルギー」は製品の「密度ρ」と「粘度η」によって決まってくると言えます。

そして，撹拌機の種類によって ，「製品に対して付与できる1秒間あたりの撹拌エネルギー」 が「吐出作用」と「微細化作用」に振り分けられます。

撹拌羽根と製品との関係を調べるうえで，これらの知見を利用できるかもしれません。

すなわち，撹拌機を使用するにあたって，「密度ρ」と「粘度η」によって製品を分類して考えると良いかもしれません。