”ギブス自由エネルギー”から”乳化”を考えてみよう

これまでに，ギブス自由エネルギーのイメージを説明してきました。

ギブス自由エネルギーを使うと，様々な自然現象が自発的に引き起こされるか否かを評価できるようになることがわかりました。

なぜ，わざわざギブス自由エネルギーのイメージを説明したかというと，実はエネルギーの側面から分散液の1つである乳化の特徴が見えてくるのです。

これまでに紹介してきた「撹拌の立場から乳化をイメージしよう【水溶液と分散液】」「撹拌の立場から乳化をイメージしよう【界面自由エネルギーの考え方】」のページを参考にして，乳化について少し踏み込んで考えてみましょう。

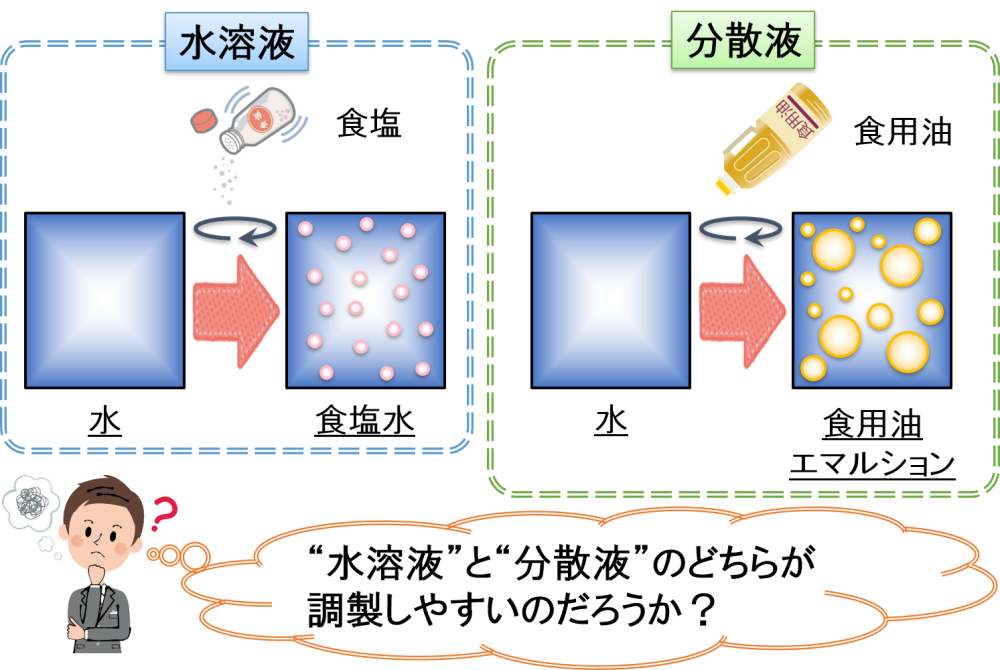
“水溶液”や“分散液”の調製しやすさ

世の中には，”水溶液”と”分散液”が存在すると紹介させていただきました。

そして，見た目は同じ液体であっても，両者には異なる点があることも併せて紹介させていただきました。

ここで論点となるのは，“水溶液”と“分散液”のどちらが調製しやすいのだろうか？…ということです。

ギブス自由エネルギーと溶解現象

水溶液の代表例として，食塩水を考えてみたいと思います。

食塩が水に溶解するという自然現象が理想混合であると考えると，溶解時におけるギブス自由エネルギーを算出することができます。

📝[memo]　理想混合することはエンタルピーの変化量が0でありエントロピーのみが変化することを意味しますが，ここではあまり気にしないでください。

📝[memo]　以下，計算ばかりが続きますが，最終的な結果だけが重要になりますので必要に応じて飛ばしてください。

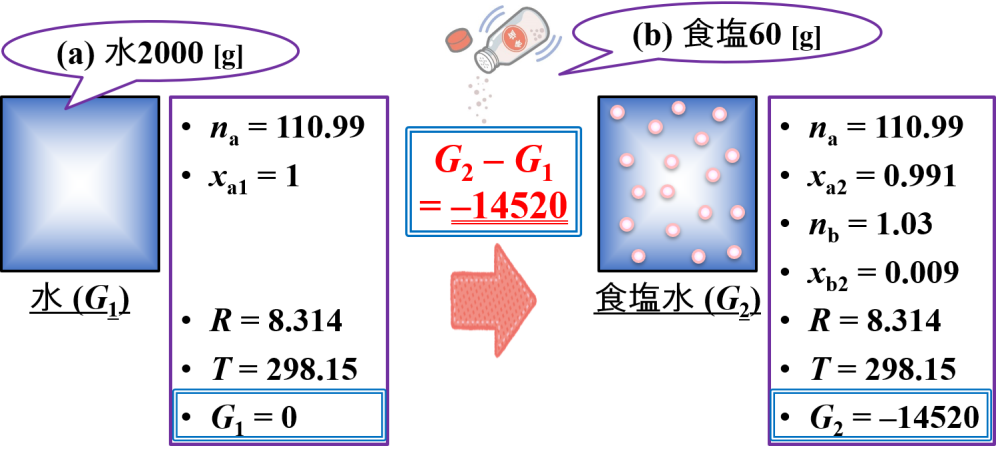
25 [℃] (T = 298.15 [K])にて，水2000 [g] に食塩（塩化ナトリウム）60 [g]を添加することを考えます。

📝[memo]　水の分子量は18.02 [mol]，塩化ナトリウムの分子量は58.44 [mol]とします。

📝[memo]　成分a＝水，成分b＝塩化ナトリウムとします。

（状態1）水のみ

• n_a = M_a/Mw_a = 2000/18.02 = 110.99
• x_a1 = n_a/n_a =110.99/110.99 = 1
• G₁ = RT(n_alnx_a1) = 8.314×298.15×(110.99×ln1) = 0

（状態2）水と食塩

• n_b = M_b/Mw_b = 60/54.88 = 1.03
• x_a2 = n_a/(n_a + n_b) = 110.99/(110.99 + 1.03) = 0.991
• x_b2 = n_b/(n_a + n_b) = 1.03/(110.99 + 1.03) = 0.009
• G₂ = RT(n_alnx_a2 + n_blnx_b2) = 8.314×298.15×(111.11×ln0.991 + 1.03×ln0.009) = –14520

G₂ – G₁ = –14520 – 0 =–14520となるので，結果として食塩水が生成すると系のギブス自由エネルギー変化は負になることがわかります。

すなわち，食塩は自発的に水へ溶解することを意味しています。

誤解を恐れず表現すると，水溶液の調製は何もしなくてもできるので“容易”であると言うことができます。

📝[memo]　工業的に時間短縮の必要がなければ，撹拌をする必要はありません。

ギブス自由エネルギーと乳化現象

それでは，分散液（エマルション）の調製の場合はどうでしょうか？

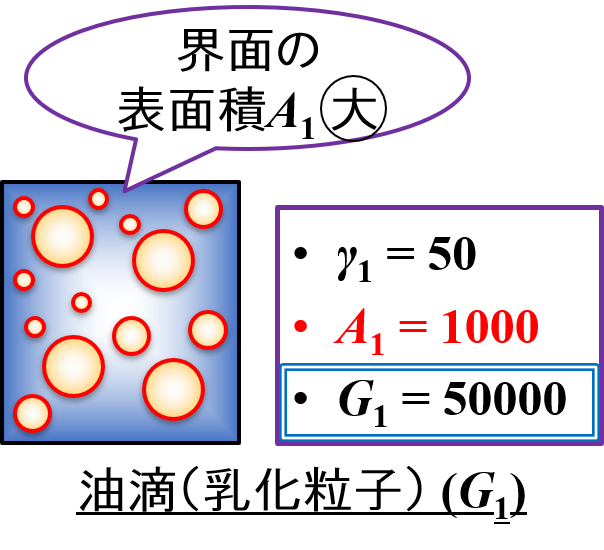
調製したエマルション（状態1）は，次のような性質を持っていると仮定します。

（状態1）界面張力γ₁

水と油の物性によって決まるので，ここでは「γ₁ = 50」とします。

📝[memo]　界面張力の解釈として，「水分子が引っ張る力と油分子が引っ張る力の差」を意味していました。

（状態1）表面積A₁

油滴となって存在しているので，ここでは「A₁ = 1000」とします。

（状態1）界面自由エネルギーG₁

界面自由エネルギーの式から，「G₁ = 50 × 1000 = 50000」と計算することができます。

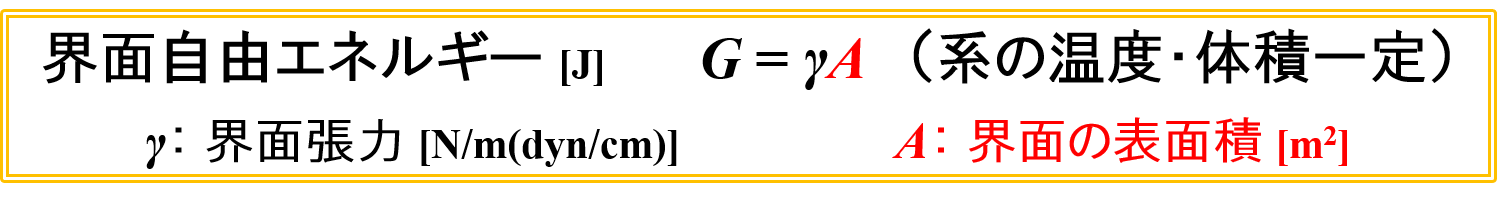
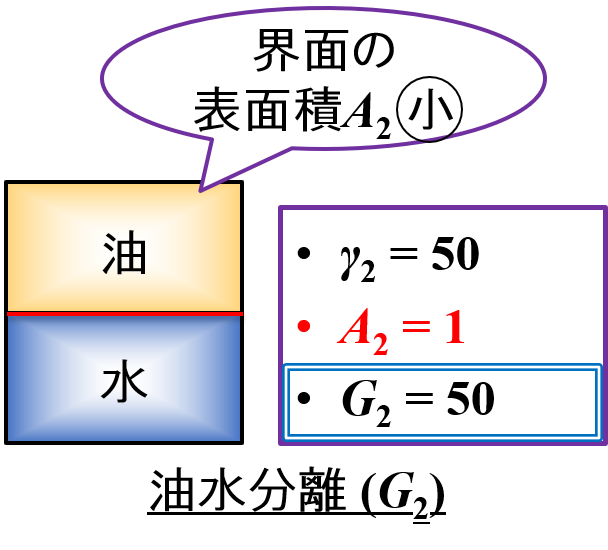
同じようにして，水と油が分離した状態（状態2）についても考えてみたいと思います。

（状態2）界面張力γ₂

エマルションの場合と同じ水と油を使用したとします。

水と油の物性によって決まるので，ここでは「γ₂ = γ₁ = 50」とします。

（状態2）表面積A₂

水と油が分離して界面の表面積が最小となっているので，ここでは「A₂ = 1」とします。

（状態2）界面自由エネルギーG₂

界面自由エネルギーの式から，「G₂ = 50 × 1 = 50」と計算することができます。

ここで，エマルション（状態1）が油水分離（状態2）するとして”ギブス自由エネルギー変化”を計算してみましょう。

（状態1）→（状態2）ギブス自由エネルギー変化ΔG

「ΔG = G₂ – G₁ = 50 – 50000 = –49950」となり，負であることがわかりました。

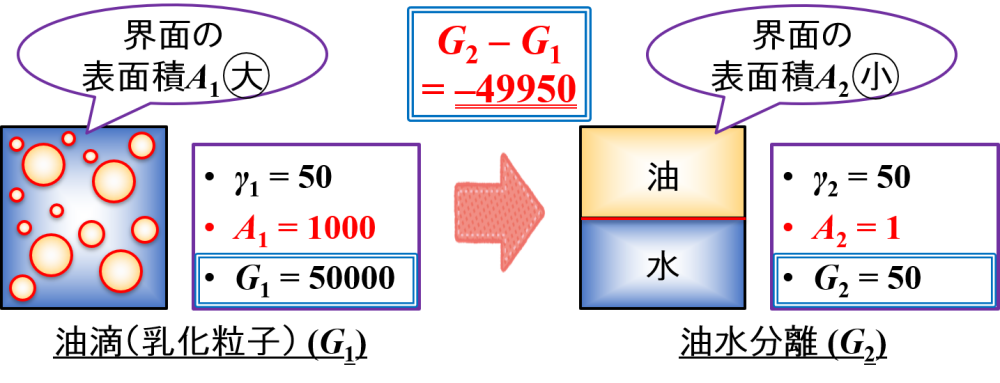
これは，エマルションが何らかの仕事をして，自発的に油水分離の状態になっていくことを意味しています。

実際の現象について注目してみると，油滴（乳化粒子）は大きな界面の表面積を持つため，自発的に油水分離が起こることがわかります。

したがって，分散液の調製は“困難”であり険しい道のりであると言えます。