界面の存在

「撹拌の立場から乳化をイメージしよう【水溶液と分散液】」のページの続きとなりますが，分散液の特徴について見ていくことにします。

見出しに，”界面自由エネルギー”という難しい言葉が出てきました。

まずは，この難しい言葉は後回しにして，我々の身近でよく見られる”界面”について考えてみたいと思います。

界面をイメージで言うと，お互いが混ざり合うことがない物質が接している境界をいいます。

水と油はお互いに混ざり合うことができないため，両者が共存する分散液中には界面が存在することを意味します。

例えば，ラーメンのスープ液面に油滴が浮いているとき，スープと油滴との間には”界面”が存在します。

このとき，異なる油滴同士をお箸でつなげると，容易に別の大きな油滴へと変化することが想像できます。

これは，油滴同士が接触するとお互いに混ざり合うことができるため，油滴間に界面は存在できないことを意味します。

厳密な定義とは少し異なる点が出てくるかもしれませんが，”界面”が存在することについてできるだけイメージできるように捉え，”界面自由エネルギー”に結びつけることをしてみましょう。

界面における”水分子”と”油分子”

ラーメンの例を出して，スープと油滴との間には”界面”が存在することを紹介しました。

ここでは，わかりやすいように単純化して，水と油が共存する場合を考えてみたいと思います。

界面付近の様子を拡大してみると，A~Cの位置に水または油分子が存在しています。

それでは，これらの分子に対して，どのような現象が引き起こされているかを見ていくことにします。

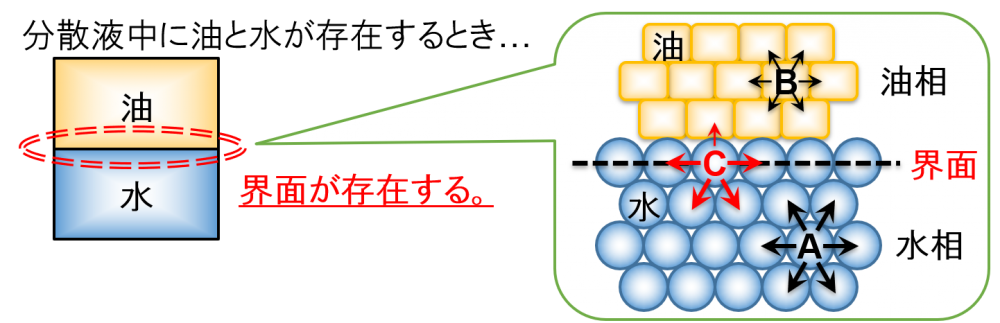
水分子A

”水分子A”は，周囲が全て同じ水分子に囲まれています。

したがって，全ての方向から等しく力を受けるために力はつり合っていると考えることができます。

油分子B

”油分子B”は，周囲が全て同じ油分子に囲まれています。

したがって，全ての方向から等しく力を受けるために力はつり合っていると考えることができます。

水分子C

”水分子C”は，上面だけ油分子と接触しています。

したがって，全ての方向から等しく力を受けているとは言えません。

実際には，引っ張る力が「油分子＜水分子」であるため，”水分子C”が下方向へ引きずり込まれることによって，界面は破壊されると考えられます。

しかしながら，我々は水と油はお互いに混ざり合うことができないため，両者が共存する分散液中には界面が存在することを知っています。

それでは，このような矛盾をどのようにして解釈したら良いでしょうか？

界面自由エネルギーの式

そこで，次のように考えることにしました。

「水と油の境界には，”界面”を作ることができるだけのエネルギーが蓄えられているのだろう。」

そして，「界面を作っている表面積」が大きくなると，それに比例して大きな「”界面”を作ることができるだけのエネルギー」が必要になりそうです。

このときのエネルギーを”界面自由エネルギー”としたわけです。

…と考えると，比例定数を用いることによって，界面自由エネルギーの式を表現できそうです。

「”界面”を作ることができるだけのエネルギー」＝「比例定数」×「界面を作っている表面積」

この比例定数は”界面張力”と呼ばれています。

この言葉自体は，これまでにどこかで聞いたことがあったのではないでしょうか？

• 「界面を作っている表面積」　→　界面の表面積A
• 「”界面”を作ることができるだけのエネルギー」　→　界面自由エネルギーG
• 「比例定数」　→　界面張力γ

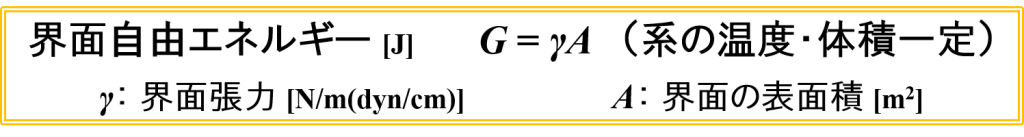
また，今回の事例では，使用した比例定数（＝界面張力γ）は「水分子が引っ張る力と油分子が引っ張る力の差」を意味しています。

「水分子が引っ張る力と油分子が引っ張る力の差」が大きいと，それに比例して大きな”界面自由エネルギー”が必要になるとも理解できそうですね。

📝[memo]　不正確な点があるかと思いますが，まずはこのようにイメージすることにしましょう。

続いて，この界面自由エネルギーから解釈できることについて考えていくことにしましょう。